For $n=2$, consider the free abelian group generated by polynomials corresponding to $\frac{(2 n)!}{2^n n!}=3$ partitions of $2n=4$ vertices into pairs (chords):
$$
(x_1-x_3)(x_2-x_4),(x_1-x_2)(x_3-x_4),(x_1-x_4)(x_2-x_3)
$$
Euler's Identity: $
(x_1-x_3)(x_2-x_4)=(x_1-x_2)(x_3-x_4)+(x_1-x_4)(x_2-x_3)$.
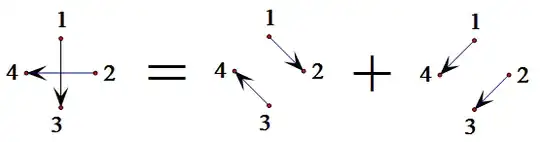
So$$\{(x_1-x_2)(x_3-x_4),(x_1-x_4)(x_2-x_3)\}\tag1\label2$$ is a basis.
So the rank of the free abelian group is $2$.
For $n=3$, consider the free abelian group generated by polynomials corresponding to $\frac{(2 n)!}{2^n n!}=15$ partitions of $2n=6$ vertices into pairs (chords):
\begin{array}r
\{(x_1-x_2) (x_3-x_4) (x_5-x_6),\\(x_1-x_2) (x_3-x_5) (x_4-x_6),\\(x_1-x_2) (x_4-x_5) (x_3-x_6),\\(x_1-x_3) (x_2-x_4) (x_5-x_6),\\(x_1-x_3) (x_2-x_5) (x_4-x_6),\\(x_1-x_3) (x_4-x_5) (x_2-x_6),\\(x_2-x_3) (x_1-x_4) (x_5-x_6),\\(x_1-x_4) (x_2-x_5) (x_3-x_6),\\(x_1-x_4) (x_3-x_5) (x_2-x_6),\\(x_2-x_3) (x_1-x_5) (x_4-x_6),\\(x_2-x_4) (x_1-x_5) (x_3-x_6),\\(x_3-x_4) (x_1-x_5) (x_2-x_6),\\(x_2-x_3) (x_4-x_5) (x_1-x_6),\\(x_2-x_4) (x_3-x_5) (x_1-x_6),\\(x_3-x_4) (x_2-x_5) (x_1-x_6)\}
\end{array}
Using Euler's Identity we can decompose the product of intersecting chords into the sum of products of the non-intersecting chords. For example $(x_1-x_4)(x_2-x_5)(x_3-x_6)$ as in Fuhrmann's Theorem,
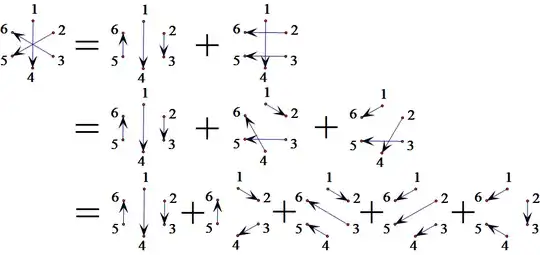There are 5 partitions of 6 vertices into non-intersecting chords
$$\tag2\label1\begin{array}l\{(x_1-x_6)(x_2-x_5)(x_3-x_4),\\ (x_1-x_6)(x_2-x_3)(x_4-x_5),\\ (x_1-x_4)(x_2-x_3)(x_5-x_6),\\(x_1-x_2)(x_3-x_6)(x_4-x_5),\\(x_1-x_2)(x_3-x_4)(x_5-x_6)\}\end{array}$$
Under lexicographic order, the leading terms of \eqref{1} are distinct: $\{x_1x_2x_3,x_1x_2x_4,x_1x_2x_5,x_1x_3x_4,x_1x_3x_5\}$. Suppose $c_1(x_1-x_6)(x_2-x_5)(x_3-x_4)+\dots+c_5(x_1-x_2)(x_3-x_4)(x_5-x_6)=0$ for some $c_1,\dots,c_5\in\mathbb{Z}$.
Comparing coefficients of term $x_1x_2x_3$ to get $c_1=0$, comparing coefficients of term $x_1x_2x_4$ to get $c_2=0$, comparing coefficients of term $x_1x_2x_5$ to get $c_3=0$, comparing coefficients of term $x_1x_3x_4$ to get $c_4=0$, comparing coefficients of term $x_1x_3x_5$ to get $c_5=0$, so $c_1=\dots=c_5=0$, \eqref{1} is linearly independent.
So the rank of the free abelian group is 5.
Here is a proof that the number of non-intersecting chords is Catalan number $\frac1{n+1}\binom{2n}n$.
Each polynomial in \eqref{1} can be written as a $2×n$ "non-intersecting tableaux" $$ \Biggl\{\begin{array}{|c|c|}\hline1&2&3\\\hline6&5&4\\\hline\end{array}, \begin{array}{|c|c|}\hline1&2&4\\\hline6&3&5\\\hline\end{array}, \begin{array}{|c|c|}\hline1&2&5\\\hline4&3&6\\\hline\end{array}, \begin{array}{|c|c|}\hline1&3&4\\\hline2&6&5\\\hline\end{array}, \begin{array}{|c|c|}\hline1&3&5\\\hline2&4&6\\\hline\end{array}\Biggr\} $$ To show that a "non-intersecting tableux" is determined by its first row, we give a procedure to fill in the second row. For example $\begin{array}{|c|c|}\hline1&2&5&7\\\hline?&?&?&?\\\hline\end{array}$ to fill $3,4,6,8$ in the second row such that there are no intersecting chords, we must put $3$ under the largest number less than $3:\begin{array}{|c|c|}\hline1&2&5&7\\\hline?&3&?&?\\\hline\end{array}$ then we must put $4$ under the largest remaining number less than $4:\begin{array}{|c|c|}\hline1&2&5&7\\\hline4&3&?&?\\\hline\end{array}$, then we must put $6$ under the largest remaining number less than $6:\begin{array}{|c|c|}\hline1&2&5&7\\\hline4&3&6&?\\\hline\end{array}$, then we must put $8$ under the largest remaining number less than $8:\begin{array}{|c|c|}\hline1&2&5&7\\\hline4&3&6&8\\\hline\end{array}$
For all $n$ we have shown the first rows of $\frac1{n+1}\binom{2n}n$ number of "non-intersecting tableaux" are distinct.
Under lexicographic order, the leading terms of \eqref{1} correspond to the first row of tableaux, so the leading terms are distinct, so the set of polynomials corresponding to "non-intersecting tableux" are linearly independent for all $n$.
So we have proved:
For all $n$, the rank of the above free abelian group in $2n$ variables is $\frac1{n+1}\binom{2n}n$.
For $n=4$, similarly decompose the product of intersecting chords into the sum of products of the non-intersecting chords. For example $(x_1-x_5)(x_2-x_6)(x_3-x_7)(x_4-x_8)$
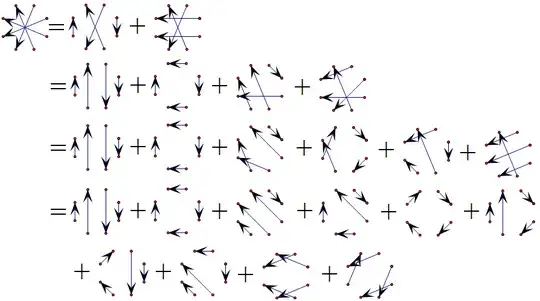
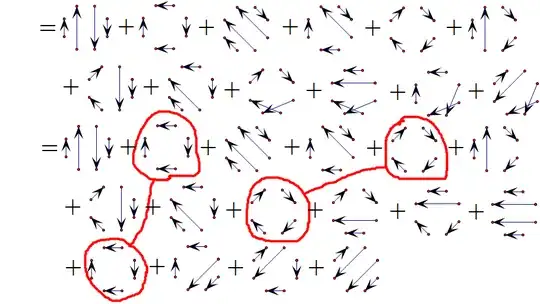As you can see, there will be two identical pairs in the end, so after collecting terms there will be two terms with coefficient $2$
\begin{align} (x_1 - x_5)(x_2 - x_6)(x_3 - x_7)(x_4 - x_8)\\
= (x_1 - x_4)(x_2 - x_3)(x_5 - x_8)(x_6 - x_7)\\
+ \color{red}{2}(x_1 - x_8)(x_2 - x_3)(x_4 - x_5)(x_6 - x_7)\\
+ (x_1 - x_2)(x_3 - x_8)(x_4 - x_7)(x_5 - x_6)\\
+ (x_1 - x_2)(x_3 - x_8)(x_4 - x_5)(x_6 - x_7)\\
+ \color{red}{2}(x_1 - x_2)(x_3 - x_4)(x_5 - x_6)(x_7 - x_8)\\
+ (x_1 - x_2)(x_3 - x_4)(x_5 - x_8)(x_6 - x_7)\\
+ (x_1 - x_4)(x_2 - x_3)(x_5 - x_6)(x_7 - x_8)\\
+ (x_1 - x_8)(x_2 - x_3)(x_4 - x_7)(x_5 - x_6)\\
+ (x_1 - x_2)(x_3 - x_6)(x_4 - x_5)(x_7 - x_8)\\
+ (x_1 - x_8)(x_2 - x_7)(x_3 - x_4)(x_5 - x_6)\\
+ (x_1 - x_8)(x_2 - x_7)(x_3 - x_6)(x_4 - x_5)\\
+ (x_1 - x_8)(x_2 - x_5)(x_3 - x_4)(x_6 - x_7)\\
+ (x_1 - x_6)(x_2 - x_3)(x_4 - x_5)(x_7 - x_8)\\
+ (x_1 - x_6)(x_2 - x_5)(x_3 - x_4)(x_7 - x_8)\end{align}
Conjecture. Express $(x_1-x_{n+1})(x_2-x_{n+2})\dots(x_n-x_{2n})$ as a linear combination of polynomials corresponding to the non-intersecting chords, then the term $(x_1-x_2)(x_3-x_4)\cdots(x_{2n-1}-x_{2n})$ and the term $(x_{2n}-x_1)(x_2-x_3)\cdots(x_{2n-2}-x_{2n-1})$ have largest coefficient in absolute value.
Mathematica code to compute the largest coefficients in absolute value
Needs["Combinatorica`"];
coeff[n_]:=Max[Abs[PolynomialReduce[Product[Indexed[x,i]-Indexed[x,n+i],{i,n}],Table[Module[{t1=t[[1]],t2=t[[2]],poly=1,i=1},Do[i=1;While[Length[t1]>i&&t1[[i+1]]<t2[[1]],i++];poly*=Indexed[x,t1[[i]]]-Indexed[x,t2[[1]]];t1=Delete[t1,i];t2=Rest[t2],n];poly],{t,Tableaux[Table[n,2]]}],Table[Indexed[x,i],{i,2n}]][[1]]]]
the terms $n=2,\dots,9$ in the sequence agree with A099960: \begin{array}{c|c} n&2&3&4&5&6&7&8&9\\\hline \text{largest abs coefficient}&1&1&2&3&8&17&56&155 \end{array}
