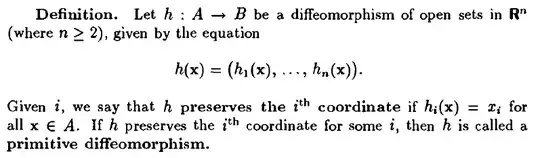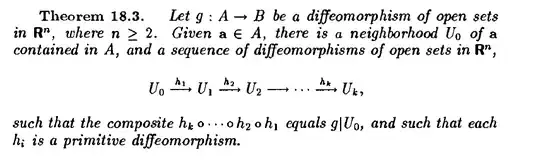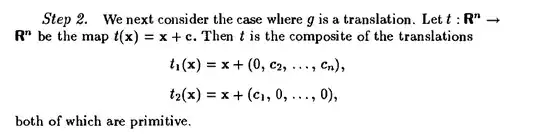I ask in this question how to solve an exercise of the text Analysis on Manifolds by James Munkres: the exercise consist to prove a theorem about diffeomorphism with more restrictive conditions. Since the solution I gave is similar to the proof of the theorem that Munkres gave for sake of completenes I put it here but if you want you can directely read my solution and when I refer to Munkres's proof you can see the step I use because I indicate it explicitely
In text Analysis on Manifolds by James Munkres there is the following definition.
So Munkres states that any diffeomorphism can be locally factorised with several primitive diffeomorphims so that he claims that the following theorem holds.
Well Munkres prove it in four sep.
So in the first step he proves that any linear transfomation is a diffeomorphism that could be factorised locally with severl primitive diffeomorphisms as you can check (if you like) to follow.
Then in the second step he proves that any traslation is a diffeomorphism that could be factorised locally with two primitive diffeomorphisms as you can check (if you like) to follow.
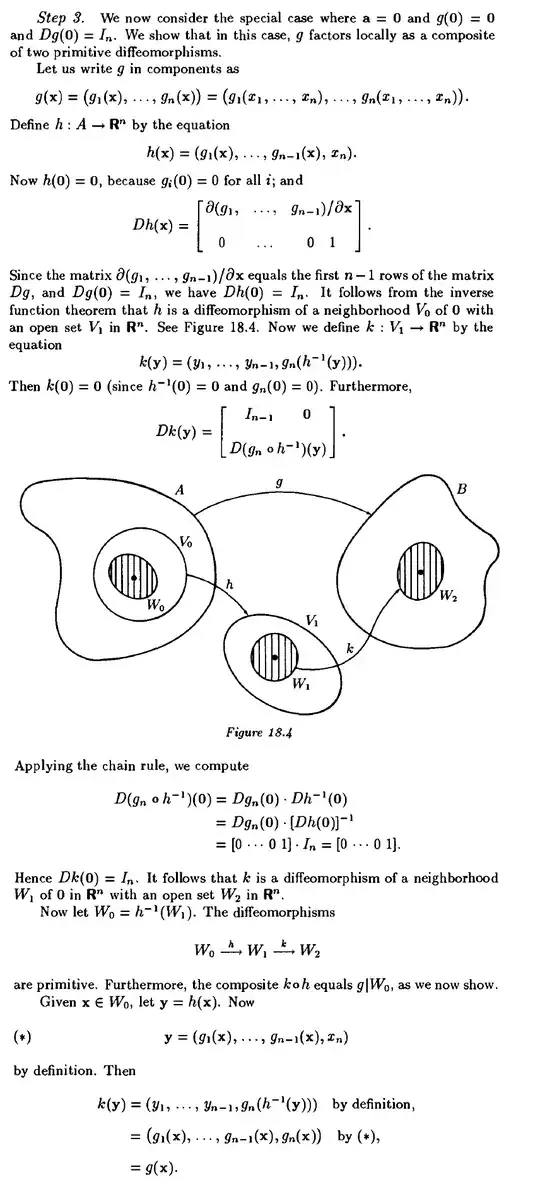
Then in the third step he proves that the theorem holds in the case where $g(0)=0$ and $Dg(0)=I_n$ as you can check (if you like) to follow.
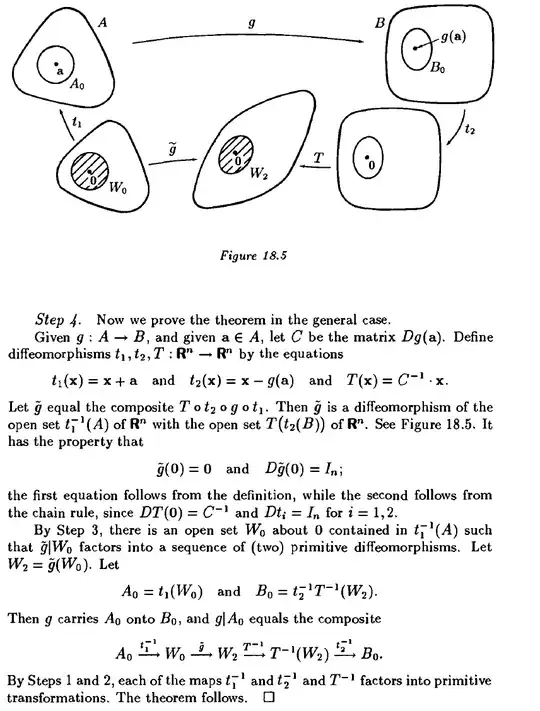
Finally in the four step he proves the general case using the preceding results.
However then as exercise Munkres ask to show that the preceding theorem holds with more restrictive definition of diffeomorphism that is he ask to prove the following statement.
So unfortunately I don't be able to use the Munkres's hit (are you able to do it?) but it seems I found the following alternative solution.
First of all we observe that any linear transmormation could be factorised with serveral primitive diffeomorphisms: indeed as you can check the elementary row operation of type $2$ and $3$ (for datail see the step $1$ of the preceding theorem) modify only the $i$-th row of a matirx and the elements of the $i$-th row of a matrix are the $i$-th components of the image of the vector of a base.
Then if $t$ is a traslation of length and direction $\pmb c:=(c_1,...,c_n)$ then for any $i=1,...,n$ we can define the primitive diffeomorphism $$ t_i(x):=(x_1,..,x_i+c_i,...,x_n) $$ and observe that $$ t(x)=x+c_1\cdot e_1+c_2\cdot e_2+...+c_n\cdot e_n= \\ =\Biggl(\Big(...\big((x+c_1\cdot e_1)+c_2\cdot e_2\big)+...\Big)+c_n\cdot e_n\Biggl)=\Biggl(\Big(...\big(t_1(x)+c_2\cdot e_2\big)+...\Big)+c_n\cdot e_n\Biggl)=\Biggl(\Big(...\big(t_2(t_1(x))\big)+...\Big)+c_n\cdot e_n\Biggl)= \\ =...=t_n\Big(...\big(t_2(t_1(x)\big)...\Big)=(t_n\,\circ...\circ\,t_1)(x) $$ so that any traslation could be factorised with serveral primitive diffeomorphisms.
Now as Munkres did we consider the special case where $a=0$, $g(0)=0$ and $Dg(0)=I_n$. So first we define the function $h_1A\rightarrow\Bbb R^n$ through the condition $$ h_1(x):=\big(g_1(x),x_2,...,x_n\big) $$ and we observe that if $g_1(0)=0$ and $Dg_1=e_1$ then $h_1(0)=0$ and $Dh_1(0)=I_n$ and so it follows form the inverse function theorem that $h_1$ is a diffeomorphism (clearly it is primitive!) of a open neighborhood $V_0$ of $0$ with an open set $V_1$ that contains $h_1(0)=0$. So now we define the function $h_2:V_1\rightarrow\Bbb R^n$ through the condition $$ h_2(y):=\Big(y_1,\big(g_2\,\circ\,h_1^{-1}\big)(y),y_2,...,y_n\Big) $$ for any $y\in V_1$ and we observe that if $g_2(0)=0$ and $Dg_2(0)=e_2$ then $g\big(h^{-1}_1(0)\big)=0$ and $Dg_2\big(h^{-1}_1(0)\big)=Dg_2\big(h^{-1}_1(0)\big)\cdot Dh^{-1}_1(0)=Dg_2(0)\cdot\big(Dh_1(0)\big)^{-1}=e_2\cdot I_n=e_2$ and so $h_2(0)=0$ and $D h_2(0)=I_n$ thus it follows form the inverse function theorem that $h_2$ is a diffeomorphism (clearly it is primitive!) of a open neighborhood $U_1$ of $0$ with an open set $U_2$ that contains $h_2(0)=0$. So the sets $$ W_0:=h^{-1}_1[U_1\cap V_1], W_1:=(U_1\cap V_1)\,\,\,\text{and}\,\,\,W_2:=h_2[U_1\cap V_1] $$ are open neighborhoods of $0$ and the function $(h_2|_{W_1}\,\circ\,h_1|_{W_0})$ is a diffeomorphism from $W_0$ to $W_2$ such that $$ (h_2|_{W_1}\,\circ\,h_1|_{W_0})(x):=h_2(h_1(x))=h_2\big((g_1(x),x_2,...,x_n)\big)=\Big(g_1(x),\big(g_2\,\circ\,h^{-1}_1\big)\big((g_1(x),x_2,...,x_n)\big),x_3,...,x_n\Big)=\Big(g_1(x),\big(g_2\,\circ\,h^{-1}_1\big)\big(h_1(x))\big),x_3,...,x_n\Big)=\Big(g_1(x),g_2\big(h^{-1}_1(h_1(x))\big),x_3,...,x_n\Big)=\big(g_1(x),g_2(x),x_3,...,x_n\big) $$ for any $x\in W_0$. So for $i<n$ we assume that $V_0,V_2,...,V_i$ is a collection of open neighborhoods of $0$ for which exist a sequence of primitive diffeomorphisms $h_1,...,h_i$ there defined such that $$ h_1(0)=h_2(0)=...=h_i(0)=0\,\,\,\text{and}\,\,\,Dh_1(0)=Dh_2(0)=...=Dh_i(0)=I_n $$ and moreover we suppose that $$ \big(h_i\,\circ...\circ\,h_2\,\circ\,h_1\big)(x)=\big(g_1(x),g_2(x),...,g_i(x),x_{i+1},...,x_n\big) $$ for any $x\in V_0$. So we define the function $h_{i+1}:V_i\rightarrow\Bbb R^n$ through the condition $$ h_{i+1}(y):=\Big(y_1,...,y_i,\big(g_{i+1}\,\circ\,h_1^{-1}\,\circ\,h_2^{-1}\,\circ...\circ\,h_i^{-1}\big)(y),y_{i+2},...,y_n\Big) $$ for any $y\in V_i$ and so we observe that if by assumption $g_{i+1}(0)=0$, $Dg_{i+1}(0)=e_{i+1}$ and if by the inductive hypothesis $h_1^{-1}(0)=h_2^{-1}(0)=...=h_i^{-1}(0)=0$ and $\big(Dh_1(0)\big)^{-1}=\big(Dh_2(0)\big)^{-1}=...=\big(Dh_i(0)\big)^{-1}=I_n$ then $$ (g_{i+1}\,\circ\,h_1^{-1}\,\circ\,h_2^{-1}\,\circ...\circ\,h_i^{-1}\big)(0)=0 $$ and
$$ D\big(g_{i+1}\,\circ\,h_1^{-1}\,\circ\,h_2^{-1}\,\circ...\circ\,h_i^{-1}\big)(0)=Dg_{i+1}(0)\cdot Dh_1^{-1}(0)\cdot Dh_2^{-1}(0)\cdot...\cdot Dh_i^{-1}(0)=e_{i+1}\cdot I_n\cdot I_n\cdot...\cdot I_n=e_{i+1} $$ so that $h_{i+1}(0)=0$ and $Dh_{i+1}(0)=I_n$ and so it follows form the inverse function theorem that $h_{i+1}$ is a diffeomorphism (clearly it is primitive!) of a open neighborhood $ U_i$ of $0$ with an open set $U_{i+1}$ that contains $h_{i+1}(0)=0$. So the sets $$ W_0:=h^{-1}_1\Big[h^{-1}_2\big[...[h^{-1}_i[U_i\cap V_i]...\big]\Big],\,W_1:=h^{-1}_2\big[...[h^{-1}_i[U_i\cap V_i]...\big],\,..., \\ W_{i-1}:=h^{-1}_i[U_i\cap V_i],\,W_i:=U_i\cap V_i\,\,\,\text{and}\,\,\,W_{i+1}:=h_{i+1}[U_i\cap V_i] $$ are open neighborhoods of $0$ and the function $(h_{i+1}|_{W_i}\,\circ\,h_i|_{W_{i-1}}\,\circ\,...\circ\,h_2|_{W_1}\,\circ\,h_1|_{W_0})$ is a diffeomorphism of $W_0$ in $W_{i+1}$ such that $$ \big(h_{i+1}|_{W_i}\,\circ\,h_i|_{W_{i-1}}\,\circ\,...\circ\,h_2|_{W_1}\,\circ\,h_1|_{W_0}\big)(x)=\big(h_{i+1}\,\circ\,h_i\,\circ\,...\circ\,h_2\,\circ\,h_1\big)(x)=\Big(h_{i+1}\,\circ\big(h_i\,\circ\,...\circ\,h_2\,\circ\,h_1\big)\Big)(x)=h_{i+1}\Big(\big(h_i\,\circ\,...\circ\,h_2\,\circ\,h_1\big)(x)\Big)=h_{i+1}\Big(\big(g_1(x),g_2(x),...,g_i(x),x_{i+1},...,x_n\big)\Big)= \\ =\Biggl(g_1(x),g_2(x),...,g_i(x),\Big(g_{i+1}\,\circ\,h_1^{-1}\,\circ\,h_2^{-1}\,\circ...\circ\,h_i^{-1}\Big)\Big(\big(g_1(x),g_2(x),...,g_i(x),x_{i+1},...,x_n\big)\Big),x_{i+2},...,x_n\Biggl)=\Biggl(g_1(x),g_2(x),...,g_i(x),\Big(g_{i+1}\,\circ\,h_1^{-1}\,\circ\,h_2^{-1}\,\circ...\circ\,h_i^{-1}\Big)\Big(\big(h_i\,\circ...\circ\,h_2\,\circ\,h_1\big)(x)\Big),x_{i+2},...,x_n\Biggl)= \\ =\Biggl(g_1(x),g_2(x),...,g_i(x),\Big(g_{i+1}\,\circ\big(h_1^{-1}\,\circ\,h_2^{-1}\,\circ...\circ\,h_i^{-1}\big)\Big)\Big(\big(h_i\,\circ...\circ\,h_2\,\circ\,h_1\big)(x)\Big),x_{i+2},...,x_n\Biggl)= \\ =\Biggl(g_1(x),g_2(x),...,g_i(x),g_{i+1}\biggl(\Big(h_1^{-1}\,\circ\,h_2^{-1}\,\circ...\circ\,h_i^{-1}\Big)\Big(\big(h_i\,\circ...\circ\,h_2\,\circ\,h_1\big)(x)\Big)\biggl),x_{i+2},...,x_n\Biggl)= \\ =\Biggl(g_1(x),g_2(x),...,g_i(x),g_{i+1}\biggl(\Big(\big(h_1^{-1}\,\circ\,h_2^{-1}\,\circ...\circ\,h_i^{-1}\big)\circ\big(h_i\,\circ...\circ\,h_2\,\circ\,h_1\big)\Big)(x)\biggl),x_{i+2},...,x_n\Biggl)= \\ =\Big(g_1(x),g_2(x),...,g_i(x),g_{i+1}(x),x_{i+2},...,x_n\Big) $$ for any $x\in W_0$. So finally by finite induction theorem we conclude that there exist a sequence $V_0,V_1,...,V_{n-1}$ of length $n$ for which exist a sequence $h_1,...,h_n$ of primitive diffeomorphism there defined,combinable and such that $g|_{V_0}\equiv h_n\,\circ...\circ\,h_2\,\circ\,h_1$.Finally with the same arguments that Munkres did in the step $4$ we conclude that the theorem holds.
So I ask if the solution I gave to exercise is correct and if not I ask to solve it. So could someone help me, please?