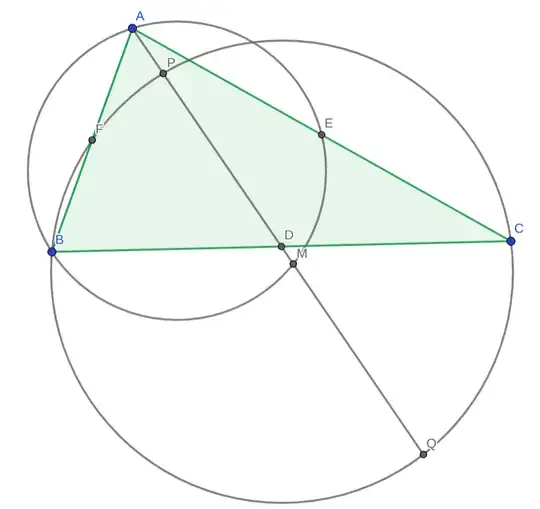
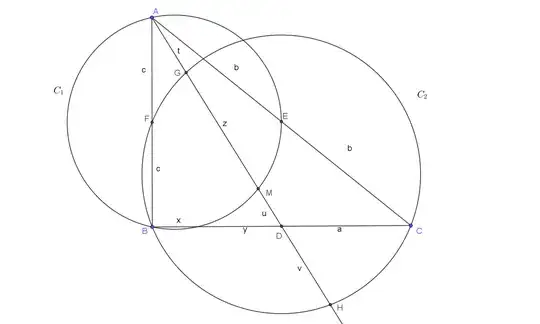
Let $\triangle DEF$ be the medial triangle of $\triangle ABC$ with standaring notations. Let $AD\cap (BFC) $ in points $P$ and $Q$ and let $AD\cap (ABE)=M$ then $MP=MQ$.
There was a non synthetic solution given here https://artofproblemsolving.com/community/c1213795h2168723p16462131
But I am interested in a synthetic solution.
Thanks in advance.