CGMO 2020: Prove that $X, P, Q, Y$ are concyclic.

Question

In the quadrilateral $ABCD$, $AB=AD$, $CB=CD$, $\angle ABC =90^\circ$. $E$, $F$ are on $AB$, >$AD$ and $P$, $Q$ are on $EF$($P$ is between $E, Q$), satisfy $\frac{AE}{EP}=\frac{AF}{FQ}$. $X, Y$ are on $CP, CQ$ that satisfy $BX \perp CP, DY \perp CQ$. Prove that $X, P, Q, Y$ are concyclic.

My Progress: Couldn't proceed much . I noted that $ABCD$ is cyclic quad with diameter $AC$ . I feel to use POP on C , so it is enough to show that $CX\cdot CP= CY\cdot CQ$ . But I am not sure about how to use "$\frac{AE}{EP}=\frac{AF}{FQ}$" criteria .

Please post hints rather than solution. It really helps me a lot.

Thanks in advance.

If $AB=BC=CD$ and $ABC$ is $90$ degree, then $ABCD$ is a square. I guess there is a typo? — cr001, Aug 10 '20 at 15:29
@AlexeyBurdin , actually picture for this is really hard to draw because of the ratios given — Sunaina Pati, Aug 10 '20 at 15:33

score 4 · Accepted Answer · answered Aug 10 '20 at 15:57

4

Here's the hint.

($1$) The colored line are of importance. Think what the color means.

($2$) Make use of parallel line ratio.

answered Aug 10 '20 at 15:57

cr001

12,778

Thanks for the hint ! – Sunaina Pati Aug 11 '20 at 04:54

score 4 · Answer 2 · answered Aug 10 '20 at 19:44

This is a full proof following the natural wish in the OP to use the power of the point $C$ w.r.t. the points that should be on the circle.

The picture first (and try to figure out a property of the line $P'Q'$ without further reading):

Here, many elements are needed only for having a faithful picture. The points needed in the proof are the red ones:

$\color{red}Z$ is the intersection of the lines $EPQF$ and $AC$,
$\color{red}{P'}$ is $AB\cap CX$, and $\color{red}{Q'}=AD\cap CY$.

We compute $CX\cdot CP$, trying to express it in a "symmetricaly way" w.r.t. the given symmetry of the figure. First, since there is a right angle in $B$ in $\Delta BCP'$ we have $$ CB^2= CX\cdot CP'\ . $$ So it is natural to try to deal with the proportion $CP:CP'$ or with some derivated form of it.

A further hint so far:

Using for instance for the equality marked $(!)$ below the sine theorem in $\Delta AEZ$ and $\Delta AFZ$ we get: $$ \tag{$1$} \frac {PE}{QF}= \frac {AE}{AF}\overset{(!)}{=\!=} \frac {ZE}{ZF}= \frac {ZP}{ZQ}\ . $$

Lemma: $$ \tag{$2$} \color{red}{P'Q'}\|EF\ . $$ Proof: Menelaos in $\Delta EAZ$ for the "secant" line $CPP'$, respectively in $\Delta FAZ$ for the "secant" line $CQQ'$ gives: $$ \begin{aligned} 1&= \frac{PZ}{PE}\cdot \color{blue}{\frac{P'E}{P'A}}\cdot \frac{CA}{CZ} \ , \\ 1&= \frac{QZ}{QE}\cdot \color{blue}{\frac{Q'E}{Q'A}}\cdot \frac{CA}{CZ} \ , \end{aligned} $$ and the middle blue proportions are equal, since the others are correspondingly. (Use $(1)$.) Thus the claimed parallelism.

$\square$

The finish is now: $$ \begin{aligned} \frac {CX\cdot CP}{CY\cdot CQ} &= \frac {CX\cdot CP'}{CY\cdot CQ'}\qquad\text{ since }PQ\|P'Q' \\ &= \frac {CB^2}{CD^2} =1\ . \end{aligned} $$ $\square$

Note: The green region suggests that we are trying to "move proportions" from the line $CPP'$ to the line $CZA$ by using conveniently triangles "based" on the one or the other line.

In the picture, the line $BX$ is with bad glasses going through $Y$, this is not the case in the hi res geogebra picture i exported... (I was needing a good position for $P,Q$, but this was breaking the position for $X,Y$...) — dan_fulea, Aug 10 '20 at 19:51

score 4 · Answer 3 · answered Aug 11 '20 at 09:52

Let $EF$ cut $AC$ at $R$. Then

$AR$ is angle bisector for $\angle EAF$ so ${AE\over AF} = {ER\over RF}$ and thus $${EP\over PR} ={FQ\over QR}\;\;\;(*)$$
Reflect $E,P$ and $X$ across $AC$, we get $E',P'$ and $X'$. Because of $(*)$ we have $E'F||P'Q$ and $Y,X',C,D$ are concyclic.
Let $\angle CDX'= \phi$, then $\angle CYX' = \phi $ and $\angle X'DA = 90-\phi$, so $\angle QYX' = 180-\phi $ and $\angle X'P'Q = \phi$ which means $X',Y , Q$ and $P'$ are concyclic.
By PoP with respect to point $C$ we see that $P,X,Y,Q$ are conyclic.

score 3 · Answer 4 · answered Aug 10 '20 at 17:23

3

enter image description here

This is a figure of the given situation in Geogebra.

Hint: We get $P'$ and $Q'$ by rotating $P$ and $Q$ about $E$ and $F$ respectively. Hence, we have $EP=EP'$ and $FQ=FQ'$.

Since, it is given that $\displaystyle\frac{AE}{PE}=\frac{AF}{FQ}$, line $P'Q'$ is parallel to $PQ$

answered Aug 10 '20 at 17:23

SarGe

3,061

I didn't understand about the rotation part..can you explain it once ? – Sunaina Pati Aug 11 '20 at 05:07
$P$ is rotated about $E$ such that the rotated point $P'$, $A$ and $E$ are collinear. Same for $Q$. Then use inverse BPT. – SarGe Aug 11 '20 at 07:25

score 2 · Answer 5 · answered Aug 11 '20 at 04:53

Thanks everyone, for their hints! I think I got the solution (using @cr001 's hint ) . I hope someone can verify this proof .

I am going to use @cr001's diagram.

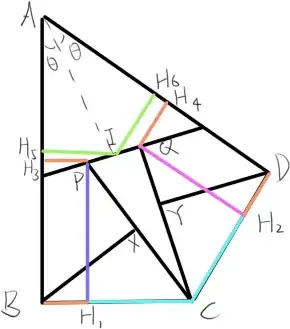
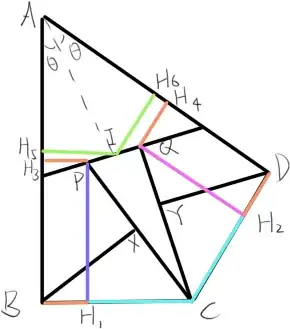
Let $AC\cap EF= I$ . Let $H_1$ be the foot of the perpendicular from $P$ to $BC$. Let $H_2$ be the foot of the perpendicular from $Q$ to $DC$. Let $H_3$ be the foot of the perpendicular from $P$ to $BA$.Let $H_4$ be the foot of the perpendicular from $Q$ to $AD$.Let $H_5$ be the foot of the perpendicular from $I$ to $BA$.Let $H_6$ be the foot of the perpendicular from $I$ to $AD$.

Now note that AI is the angle bisector of EF. So we have $\frac {AE}{AF}=\frac {EI}{IF}$ (using the angle bisector theorem )

Also we have $\frac {EP}{EI}=\frac {PH_3}{IH_5}$ (using similarity ).

similarly, we have $\frac {FQ}{FI}=\frac {QH_4}{IH_6}$ (using similarity ).

So we have $\frac {IH_5}{PH_3} \cdot\frac {QH_4}{IH_6}= \frac {EI}{EP}\cdot\frac {FQ}{FI}=\frac {AE}{EP}\cdot \frac {FQ}{AF}=1 \implies \frac {IH_5}{PH_3} \cdot\frac {QH_4}{IH_6}=1 \implies QH_4= PH_3$ (since $IH_5=IH_6$).

So we have $DH_2=QH_4= PH_3=BH_1 \implies CH_1=CH_2$ .

Now, since $\angle PH_1B=\angle BXP=90 $, we get $PH_1BX$ cyclic .

Similarly $QYH_2D$ is cyclic.

So $\Bbb P(C,(PH_1BX))= CH_1\cdot CB=CH_2\cdot CD=\Bbb P(C,(PH_1BX))$

So $\Bbb P(C,(PH_1BX))=\Bbb P(C,(QH_2YD)) \implies CX \cdot CP=CY \cdot CQ \implies XYPQ$ is cyclic .

And we are done!

CGMO 2020: Prove that $X, P, Q, Y$ are concyclic.

5 Answers5