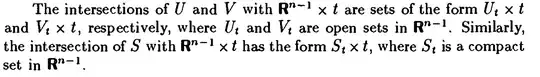0

At the page 166 of the text "Analysis on Manifolds" by James Munkres is stated if $U$ and $V$ are S set of $\Bbb R^n$ and $S$ is a compact set of $\Bbb R^n$ then it is true what following shown

enter image description here

To prove what above is stated I proceed as follow.

First of all we observe that the restriction $\phi$ of the projection $\pi_{\Bbb R^{n-1}}$ of $\Bbb{R}^{n-1}\times\Bbb R$ to the subspace $\Bbb R^{n-1}\times\{t\}$ is a homeomorphism of $\Bbb R^{n-1}\times\{t\}$ in $\Bbb R^{n-1}$ (to see this it is sufficient to observe that $\phi$ is bjective and then open and continuous too since the projection $\pi_{\Bbb R^{n-1}}$ is open and continuous) and then $\phi$ aree with the projection $\tilde\pi_{\Bbb R^{n-1}}$ of $\Bbb R^{n-1}\times\{t\}$ to $\Bbb R^{n-1}$ and so if $U_t:=\phi\big[U\cap(\Bbb R^{n-1}\times\{t\})\big]$ then $U\cap(\Bbb R^{n-1}\times\{t\})=\phi^{-1}[U_t]=\big(\tilde\pi_{\Bbb R^{n-1}}\big)^{-1}[U_t]=U_t\times\{t\}$. Similarly whit the same argument $V\cap(\Bbb R^{n-1}\times\{t\})=V_t\times\{t\}$. Then if $\pi_{_\Bbb R}$ is the projection on $\Bbb R$ of $\Bbb R^{n-1}\times\Bbb R$ then $\big(\pi_{_\Bbb R}\big)^{-1}\big[\{t\}\big]=\Bbb R^{n-1}\times\{t\}$ is closed and so the set $S\cap(\Bbb R^{n-1}\times\{t\})$ is compact so that $S_t:=\phi\big[S\cap(\Bbb R^{n-1}\times\{t\})\big]$ is compact in $\Bbb R^{n-1}$ and so as above $S\cap(\Bbb R^{n-1}\times\{t\})=\phi^{-1}[S_t]=\big(\tilde\pi_{\Bbb R^{n-1}}\big)[S_t]=S_t\times\{t\}$.

Is is my argument correct? If not how to prove what Munkres state? Then if $U$ is open is true that $U\cap(\Bbb R^{i-1}\times\{t\}\times\Bbb R^{n-i})=U'_t\times\{t\}\times U''_t$ where $U'_t$ and $U''_t$ are respectively open in $\Bbb R^{i-1}$ and in $\Bbb R^{n-i}$ and similarly if $S$ is compact then $S\cap(\Bbb R^{i-1}\times\{t\}\times\Bbb R^{n-i})=S'_t\times\{t\}\times S''_t$ where $S'_t$ and $S''_t$ are respectively compact in $\Bbb R^{i-1}$ and in $\Bbb R^{n-i}$? So could someone help me, please?

Antonio Maria Di Mauro
  • 5,226
  • So, in short, the Munkres quote is correct, but your title question is false. Wrong attempt at generalisation; can happen. – Henno Brandsma Aug 09 '20 at 21:46
  • I conjectured it for understand why the assumption that the primitive diffeomorphism $h$ defined by Munkres in the step $5$ of the proof of change of variables thorem preserves the last coordinate don't damage the generality of the proof: precisely Munkres says that this assumption is only for convenience in notation. So I prove to apply Munkres's argument to the case where $h$ preserve a general coordinate but unfornutately it seems that the it is not possible to proceed in analogous way. – Antonio Maria Di Mauro Aug 10 '20 at 22:20
  • However with a symmetrical argument which we promoted above it is possible to conclude that $U\cap({t}\times\Bbb R^{n-1})={t}\times U_t$ (IS THIS TRUE?) so that it is possible to apply the Munkres argument at the case where $h$ preserve the first coordinate. So by exercise $2$ of page $160$ it is clear that any diffeomorphism preserve or the first or the last coordinate so that the change of variables theorem follows form this two particular cases. – Antonio Maria Di Mauro Aug 10 '20 at 22:20
  • 1
    yes $t$ in the first coordinate only also works. But that doesn’t help towards more general cases. – Henno Brandsma Aug 10 '20 at 22:23
  • Excuse me but I don't understand what shall help in the general cases. Forgive my confusion. – Antonio Maria Di Mauro Aug 10 '20 at 22:24
  • Could you explain, please? – Antonio Maria Di Mauro Aug 10 '20 at 22:27
  • 1
    Well, it's obvious the question in the title is false, while Munkres' paragraph from 166 is true. – Henno Brandsma Aug 10 '20 at 22:33
  • Surely! Anyway thanks too much for your assistance!!! – Antonio Maria Di Mauro Aug 10 '20 at 22:35

1 Answers1

2

In your previous post we already saw that $h: \Bbb R^{n-1} \to \Bbb R^n$ defined by $h(x)=(x,t)$ (making obvious identifications) is a homeomorphism of $\Bbb R^{n-1}$ with $\Bbb R^{n-1} \times \{t\}$, with the projection $p$ to the first $n-1$ coordintes being the inverse.

It's then clear that if $S$ is compact in $\Bbb R^n$ then its intersection with $\Bbb R^{n-1} \times \{t\}$ is compact in $\Bbb R^{n-1} \times \{t\}$ (we use $T_1$ ness of the reals etc.) and so it is of the form $S' \times \{t\}$ with $S'= p[S] \subseteq \Bbb R^{n-1}$. The same holds, mutatis mutandis, for open sets.

Antonio Maria Di Mauro
  • 5,226
Henno Brandsma
  • 250,824
  • Okay and so this is only true for $U\cap(\Bbb R^{n-1}\times{t})$ and unfortunately not for $U\cap(\Bbb R^{i-1}\times{t}\times\Bbb R^{n-i})$ too, right? – Antonio Maria Di Mauro Aug 09 '20 at 11:43
  • @AntonioMariaDiMauro No, you cannot claim two open sets, as you did before. – Henno Brandsma Aug 09 '20 at 11:44
  • 2
    @AntonioMariaDiMauro - $\Bbb R^{n-1}\times{t}$ is isomorphic to $\Bbb R^{i-1}\times{t}\times\Bbb R^{n-i}$ by expressing $\Bbb R^{n-1} = \Bbb R^{i-1}\times \Bbb R^{n-i}$ and rearranging the coordinates. By trying to claim $U\cap(\Bbb R^{i-1}\times{t}\times\Bbb R^{n-i})=U'_t\times{t}\times U''_t$, you are claiming that $U_t = U_t' \times U_t''$, which is not true for most subsets of $\Bbb R^{n-1}$, whether open, compact, or in general. – Paul Sinclair Aug 09 '20 at 20:39