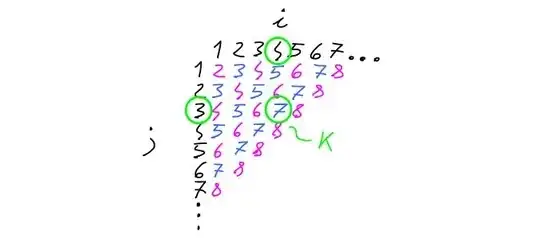Does $\sum_{i,j\in \mathbb{N}} \frac{1}{(i+j)^2}$ exist?

Question

Does $\sum_{i,j \in \mathbb{N}} \frac{1}{(i+j)^2}$ exist?

I tried with $ \frac{(i+j)}{2}\ge \sqrt{ij} $ but this seem to be of no work as for each fixed $i$, $\sum_{j} \frac{1}{ij}$ does not exist. We need a better estimate. But I can not find one.

Thanks a lot for your help.

In title and first line your question has denominator $(j+j)^2$ but sum is over all $i,j$ --- is that really what you mean? — coffeemath, Aug 05 '20 at 11:43
This notation is meaningless if you don't say where $i$ and $j$ live. — Bernard, Aug 05 '20 at 11:47
In which order are you summing? But I think it cannot converge see it by replacing your sum with integral $1\leq x,y\leq \infty$ — Guy Fsone, Aug 05 '20 at 16:06

score 4 · Accepted Answer · answered Aug 05 '20 at 15:15

Hint: As all the terms are positive, we get that the series converges iff any of its reorderings converges. Thus, we can collect all the $(i,j)$ which add up to $p$ and sum over all $p$, i.e. $$ \sum_{i,j\in \mathbb{N}_{\geq 1}} \frac{1}{(i+j)^2} = \sum_{p\in \mathbb{N}_{\geq 1}} \frac{\vert \{ (i,j)\in (\mathbb{N}_{\geq 1})^2 \ : \ i+j=p\} \vert }{p^2}. $$ Can you finish from here?

score 4 · Answer 2 · answered Aug 05 '20 at 15:53

4

HINT

By double counting we have that

$$\sum_{i,j=1}^\infty \frac{1}{(i+j)^2}= \sum_{k=2}^\infty\frac{k-1}{k^2}$$

answered Aug 05 '20 at 15:53

user

162,563

Does $\sum_{i,j\in \mathbb{N}} \frac{1}{(i+j)^2}$ exist?

2 Answers2