6

As how integration by parts has the picture below, what would the picture for partial fractions look like?

enter image description here

Although there's probably no way to escape the heavy algebra necessary for partial fractions, is there a intuitive or geometric visualization of partial fractions? And is there one that doesn't rely on animated pictures?

The closest thing that seems are those diagrams where kids do basic operations on fractions by colouring in boxes like enter image description here.

And so, for partial fractions, each of those coloured sections would be different rational functions. Probably would be hard or impossible to generalize though.

  • 2
    Can you explain how the first diagram represents integration by parts? – Sarvesh Ravichandran Iyer Aug 06 '20 at 05:48
  • @астонвіллатересалисбон have you seen the Wikipedia entry? https://en.wikipedia.org/wiki/Integration_by_parts#Visualization –  Aug 06 '20 at 08:20
  • Maybe start by drawing a second curve for one of the partial fractions (say below the original) and the difference between the two curves is implicitly the other partial fraction. This cuts the red region into two regions: one for each partial fraction. (I'd would have written this up as an answer if I were good at drawing.) – Sherwin Lott Aug 06 '20 at 12:53
  • Both graphics strike me as bad or irrelevant analogies for partial fraction decomposition. I think the only "geometric" intuition present is the idea of "size" in the context of blow-ups at points - if $R(z)$ is a rational function with a pole at $a$, then $R(z)\sim c/(z-a)^n$ for some constant $c$ and power $n$, then you can subtract $R(z)-c/(z-a)^n$ and if it still has a pole there it must have order less than $n$. One may keep proceeding in this fashion. After you've subtracted such terms, and $R(z)$ has no poles, it's a polynomial. – anon Aug 09 '20 at 02:13
  • 1
    Note that partial fraction decomposition also applies to rational numbers, but with prime power denominators. For instance $$ \frac{103}{72} = \frac{7}{8} + \frac{5}{9} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{3} + \frac{2}{9}. $$ This suggests the phenomenon is inherently algebraic, not geometric. (Also it implies the quotient group $\Bbb Q/\Bbb Z$ is a direct sum of Prufer subgroups $\Bbb Q_p/\Bbb Z_p=\Bbb Z[1/p]/\Bbb Z$, where $\Bbb Q_p,\Bbb Z_p$ are $p$-adic numbers and $p$-adic integers respectively.) Primes are like linear factors $(z-a)$. – anon Aug 09 '20 at 02:27
  • @runway44 I would suggest the key insight of modern algebraic geometry is that all of commutative algebra is geometric. Certainly localization is literally an algebraic operation, but the idea is fundamentally geometric, see e.g. https://math.stackexchange.com/a/350082/86777 – Joshua P. Swanson Aug 11 '20 at 00:14
  • @JoshuaP.Swanson That is the dominant view, but I think the word "geometric" is understood more metaphorically than literally in this sentiment, at least compared to a more casual understanding of the word "geometric" referring to stuff we can draw literal pictures of. Algebraic geometry, or what I know of it, often strikes me as distilling algebraic features out of a geometric setting and transplanting them into other settings and calling the result geometric. – anon Aug 11 '20 at 06:41
  • @runway44 Well, the affine scheme equivalent to a commutative ring is pretty literally geometric. It's a topological space with local rings of functions. In any case, it's much more than a loose analogy or metaphor. Perhaps you can't always draw a picture, but you can imagine a real manifold or variety and have a shockingly good sense for what going on. The pictures in my answer below are exactly in this spirit: I drew the case of the complex line, and it transfers to other algebraic curves through the standard dictionary. – Joshua P. Swanson Aug 11 '20 at 10:14

1 Answers1

4

I don't know exactly what qualifies as an answer here, but the picture in my head that goes along with partial fractions is just the usual picture of rational singularities in the complex plane.

For instance, $\frac{1}{z^2-9}$ has singularities at $z=\pm 3$, while $\frac{1}{z -3}$ only has a singularity at $z=3$. When plotting the modulus of this function in the complex plane, this is obvious:

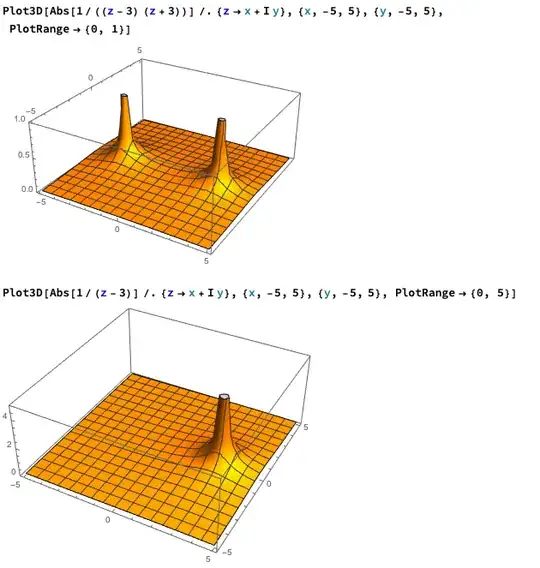
singularities

Clearly to get the pictures to look the same at all you'll need to add something like $\frac{1}{z+3}$ to $\frac{1}{z-3}$--that'll at least make sure they blow up at the right points. Moreover you can't use other denominators since then they'd blow up at the wrong places.

Near a singularity, the function is totally dominated by that singularity, so the orders of the singularities have to match up. For instance, if you start with $\frac{1}{(z-3)^2(z+3)}$, you'll definitely need to use a summand like $\frac{1}{(z-3)^2}$ and not just $\frac{1}{z-3}$, and also $\frac{1}{(z-3)^3}$ blows up "too much" so you'd need to avoid that.

Of course, if you add up $\frac{1}{(z-3)^2}$ and $\frac{1}{z-3}$ you'll get something subtly different from either, so you'll need to "keep around" the lower order terms.

Altogether, this seems like a pretty good "visual" justification for

$$\frac{p(z)}{\prod_{i=1}^n (z-\zeta_i)^{a_i}} = \sum_{i=1}^n \sum_{j=1}^{a_i} \frac{\alpha_{ij}}{(z-\zeta_i)^j}.$$

The fact that it works purely algebraically outside of the algebraically closed case or when you haven't split the denominator into linear factors is not hard to prove, of course, and you can get intuition for those versions from this one.

(For the record, at a glance I did not find the integration by parts picture intuitive. I find the product rule intuitive and that is my justification for integration by parts.)

Joshua P. Swanson
  • 11,644