What is the shortest distance you have to travel to reach where the other person was initially(12 ft apart)?

Question

You are 12ft away from a person walking towards you. He will keep walking straight, even in these COVID times. But you want to keep a minimum 6ft distance at all times.

Both are walking at the same speed at all times. And you can take any path. But he will move along the straight line joining the 2 points.

What is the shortest distance you have to travel to reach where the other person was initially (12 ft apart)?

Answer 1

Here is a better solution than just walking along a half-circle of radius $6$:

Let $A$ and $I$ be the positions of the two people initially, and let the other person be at $I$, moving towards $A$ in a straight line. Then person $A$ can move along the path $AFJI$, as shown in the diagram:

Let $\angle FAB$ be a $60º$ angle. Therefore $\sin 60º = \frac{6}{AF}$, and $AF = \frac{6}{\sin 60º} = \frac{12 \sqrt 3}{3} = 4 \sqrt 3$. $J$ is a point which is defined by $CF + FJ = DB$ and $JI$ being tangent to the circle with centre $B$ and radius $6$. But $FJ$ and $JI$ are now hard to calculate. Therefore, let $J'$ be the point $(6,6)$, where the path now is longer than with $JI$. Then $FJ'$ is $3$ units long, and $IJ'$ is $6 \sqrt{2}$ units long, for a distance of at most $4 \sqrt{3} + 6 \sqrt{2} + 3 \approx 18.4$, less than $6 \pi \approx 18.8$. GeoGebra gives the total path length as approximately $17.79$.

For a demonstration that the distance between $A$ and $B$ is always greater than $6$ feet, check out this GeoGebra demonstration here.

Answer 2

The shortest distance is about 17.45.

Take the unit distance to be 6 feet, and let their speed also be unit.

Take $B$ to be at relative rest at $(0,0)$. In this picture, $A$ starts at the point $(-2,0)$ and ends at a point $(t,0)$ where $t$ is the final distance between $A$ and $B$, equal to the length actually travelled by $A$. From $B$'s viewpoint, the path taken should be a straight line along a tangent to the unit circle, then an arc, and then another straight line to $C$. In the original true picture, $A$ moves along a line then along a curve that stays on the border of $B$'s moving unit circle and then moves in a straight line again (see diagram at bottom).

In the original picture, when $A$ moves at unit speed in direction $(\cos\theta,\sin\theta)$, then in the second picture, its velocity becomes the vector $$\begin{pmatrix}1+\cos\theta\\\sin\theta\end{pmatrix}=2\cos(\theta/2)\begin{pmatrix}\cos(\theta/2)\\\sin(\theta/2)\end{pmatrix}$$ Conversely, to go from the second picture to the original, the path's tangent vector of $(\cos\theta,\sin\theta)$ becomes $\frac{1}{2\cos\theta}(\cos2\theta,\sin2\theta)$.

There are four parts of the shortest path.

1. The tangent at angle $30^\circ$ to the unit circle. Its length in the second picture is $\sqrt3$ but in the true picture it is $\frac{\sqrt3}{2\cos30^\circ}=1$ (in the direction of $2\times30^\circ=60^\circ$).

2. The circular arc along the unit circle up to the vertical. Its true length is $$\int_0^{\pi/6}\frac{1}{2\cos\theta}d\theta=\tfrac{1}{2}[\ln(\sec\theta+\tan\theta)]_0^{\pi/6}=\tfrac{1}{4}\ln3$$

3. The circular arc from the vertical by some angle $\theta$. Its true length is $$\tfrac{1}{2}\log(\sec\theta+\tan\theta)$$

4. The straight line to $C$. Its true length is $\cot\theta/2\cos\theta=1/2\sin\theta$.

The final condition is that the total length of the path is $BC=t=1/\sin\theta$.

$$1+\tfrac{1}{4}\log3+\tfrac{1}{2}\log(\sec\theta+\tan\theta)+\frac{1}{2\sin\theta}=\frac{1}{\sin\theta}$$

This can be solved numerically: $\theta\approx0.351068$.

With this angle, the total length is $$\frac{1}{\sin\theta}=2.90782 \mathrm{units} = 17.4469 \mathrm{feet}$$

=================================================

Edit To clarify, when person $A$ comes at a distance of $1$ unit from $B$, they move along a curve that is not circular but is a translated version of the following curve: $$x'(t)^2+y'(t)^2=1,\qquad(x(t)-t)^2+y(t)^2=1,\quad (x(0),y(0))=(0,1)$$

The curve is related to the tractrix, except that it has unit speed all along. Only relative to a fixed $B$, does it appear circular.

Answer 3

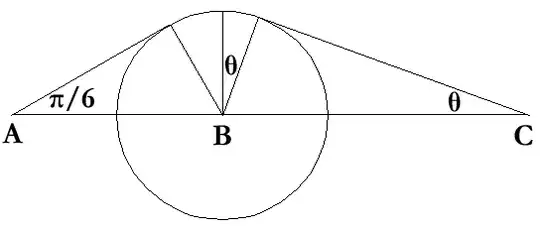
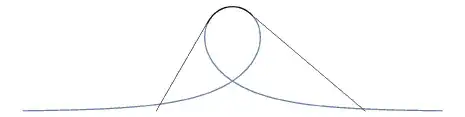
Note: This answer shows how to describe similar approach/avoidance problems using a polyline, i.e. a path composed of straight line segments.

If we use a coordinate system where initially we are at $(0, 0)$ and the other person is at $(12, 0)$, then walking in three straight line segments, $$\begin{array}{c|c|c} \text{ From } & \text{ To } & \text{ Distance } \\ \hline (0, 0) & (2\sqrt{3}, 6) & 6.92820323 \\ (2\sqrt{3}, 6) & (4.7939891, 6) & 1.32988748 \\ (4.7939891, 6) & (12, 0) & 9.37691810 \\ \end{array}$$ we reach $(12, 0)$ by walking $17.635\text{ ft}$ ($17.635009\text{ ft}$).

If we use $\bigr(x(d),y(d)\bigr)$ for our position at distance $d$, and $(12 - d, 0)$ for the position of the other person, $\bigr(x(d) - z(d)\bigr)^2 + \bigr(y(d)\bigr)^2 \ge 6$ for $d \in \mathbb{R}$.

We can parametrize the path as a polyline, using $$\left\lbrace ~ \begin{aligned} x(d) &= \frac{(d_{i+1} - d) x_i + (d - d_i) x_{i+1}}{d_{i+1} - d_i} \\ y(d) &= \frac{(d_{i+1} - d) y_i + (d - d_i) y_{i+1}}{d_{1+1} - d_i} \\ \end{aligned} \right ., \quad d_i \le d \le d_{i+1} \tag{1}\label{None1}$$ where $d$ is the distance traveled, $x(d_0) = x_0$, $x(d_1) = x_1$, $y(d_0) = y_0$, $y(d_1) = y_1$, if $$d_1 - d_0 = \sqrt{ (x_1 - x_0)^2 + (y_1 - y_0)^2 } \tag{2}\label{None2}$$ For this suggested solution, we have three line segments ($i = 0, 1, 2$) and $$\begin{array}{c|c|c|c} i & x_i & y_i & d_i \\ \hline 0 & 0 & 0 & 0 \\ 1 & 2\sqrt{3} & 6 & 6.92820323 \\ 2 & 4.7939891 & 6 & 8.25809071 \\ 3 & 12 & 0 & 17.63500881 \\ \end{array} \tag{3}\label{None3}$$ Feel free to verify $\eqref{None2}$ using the shown values; they do match.

The separation distance squared $S(d)$ is $$S_i(d) = \bigr( x(d) - z(d) \bigr)^2 + y(d)^2 \tag{4a}\label{None4a}$$ which is a quadratic function in $d$, $$S_i(d) = W_i d^2 + V_i d + U_i \tag{4b}\label{None4b}$$ where $$\begin{aligned} W_i &= \frac{(x_{i+1} - x_i + d_{i+1} - d_0)^2}{(d_{i+1} - d_i)^2} \\ V_i &= \frac{ 2 (d_{i+1} y_i - d_i y_{i+1}) (y_{i+1} - y_i) + 2 (d_{i+1} x_i - d_i x_{i+1})(x_{i+1} - x_i) } { (d_{i+1} - d_i)^2 } \\ ~ &+ \frac{ 2 (d_{i+1} + 12) x_i - 2 (d_i + 12) x_{i+1} }{ d_{i+1} - d_i } - 24 \\ U_i &= \frac{ (d_i y_{i+1} - d_{i+1} y_i)^2 + (d_i x_{i+1} - d_{i+1} x_i)^2 }{ (d_{i+1} - d_i)^2 } \\ ~ &+ \frac{ 24 d_i x_{i+1} - 24 d_{i+1} x_i }{ d_{i+1}-d_i } + 144 \\ \end{aligned} \tag{4c}\label{None4c}$$ If $$L_i \le \frac{-V_i}{2 W_i} \le L_{i+1}, \quad W_i \gt 0, \quad V_i \lt 0 \tag{4d}\label{None4d}$$ then the separation distance has a minimum at $-V_i/2 W_i$. This is true for all three line segments. The squared separation distance at that point is $$\min S_i = U_i - \frac{V_i^2}{4 W_i} \ge 6^2 \tag{4e}\label{None4e}$$ For this suggested minimum path, $$\begin{array}{c|c|c|c|c|c} i & W_i & V_i & U_i & \frac{-V_i}{2 W_i} & \sqrt{U_i - \frac{V_i^2}{4 W_i}} \\ \hline 1 & 3 & -36 & 144 & 6 & 6 \\ 2 & 4 & -61.8564067 & 275.1384396 & 7.7320508 & 6 \\ 3 & 3.5369679 & -62.3744595 & 310.993536 & 8.8175044 & 6 \\ \end{array} \tag{4f}\label{None4f}$$ i.e., we come to within the minimum allowed distance three times during the walk, after walking $6$, $7.73$, and $8.82 \text{ ft}$, but keep further away than that for the rest of the walk.

Again, feel free to verify these.

This approach can be generalized to numerically evaluate any similar problem with the path described using a polyline, i.e. a continuous curve formed from line segments. In such cases, note that when $\eqref{None4d}$ is not true, the minimum distance is reached at the path vertices, so the separation distance need to be verified there too. (In this case, the distances at the path vertices are $12$, $6.211657$, $6.091541$, and $17.63501$, and did not need to be verified because $\eqref{None4d}$ is true for all path segments.)

In general, an optimum polyline path is such that every line touches the (moving) exclusion zone. It is not always trivial to decide how many line segments are needed, or how to place them, however. So, perhaps this method is better described as showing how to verify and minimise the length of a candidate path.

---

In this particular case, for all deflection angles $\theta$ (away from the ongoing walker, $0° \lt \theta \lt 90°$), the first minimum distance case happens when both have walked $6\text{ ft}$. This may be surprising, but it is a direct consequence of $$\begin{aligned} x(d) &= d \cos\theta \\ y(d) &= d \sin\theta \\ z(d) &= 12 - d \\ s(d) &= \bigr( x(d) - z(d) \bigr)^2 + y(d)^2 \\ ~ &= 2 d^2 (1 + \cos\theta) - 24 d (1 + \cos\theta) + 12^2 \\ \end{aligned}$$ The derivative of $s(d)$ is zero at $t$, $$\frac{d s(d)}{d d} = (d - 6)(1 + \cos\theta) = 0 \quad \iff d = 6$$ and the distance at that point is $$\sqrt{s(6)} = 6\sqrt{2}\sqrt{1 - \cos\theta}$$ For that to match $6$, $$6\sqrt{2}\sqrt{1 - \cos\theta} = 6 \quad \iff \quad \cos\theta = \frac{1}{2}$$ i.e. $\theta = 60°$. So, the initial part of the initial line is fully determined by the situation.

It also gives a good guideline on how to efficiently pass oblivious people (assuming roughly the same walking speeds): divert your direction initially by $60°$, and walk in that direction until the separation is halved. Proceed from there.

---

Below is a small Python program (CC0-1.0 aka Public Domain) that starts with the fully defined initial line segment, then keeps to the $6\text{ ft}$ separation until it has a direct line of sight to the target. The total distance is $17.446895\text{ ft}$. The curved part is, like Crystomath answered, not circular or elliptic. The actual path taken:

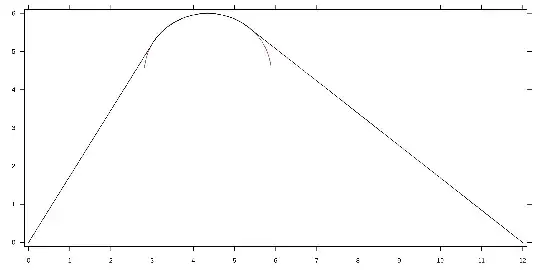
The red part is a circular approximation of the arc, with radius $1.539033\text{ ft}$ and center at $(4.352082\text{ ft}, 4.460968\text{ ft})$, just to show how close the arc is to a circle – the absolute error is less than $0.007762\text{ ft}$ (less than an eighth of an inch, or about $2.4\text{ mm}$).

The path contains three parts. It begins with the initial line segment from $(0, 0)$ to $(3, 3\sqrt{3}) \approx (3, 5.196152)$. There it continues with at least $C^1$ continuity, as a near-circular curve, to $(5.339950, 5.634042)$. (At $(4.352082, 6)$ the curve has the maximum $y$ coordinate, and that's where the two walkers have the same $x$ coordinate.) The path is completed with a final line segment to $(12, 0)$. The lengths of the respective segments are $6\text{ ft}$, $2.723439\text{ ft}$, and $8.723457\text{ ft}$.

The actual path was generated using the below Python code. It uses a configurable step size s (currently set at $1/64$th of an inch, or $1/(12\cdot 64)\text{ ft}$), with the polyline vertices at exactly $6 \text{ft}$ separation from the other person. Given short enough steps, this will yield a very precise approximation of the actual path.

from math import sqrt, sin, cos, pi
def distance(x, y):
    return sqrt(xx + yy)
def other(d):
    return 12.0-d, 0
def avoid(x, y, other_x, other_y, separation, step=1.0/1024, dymin=-1.0, dymax=1.0):
    d2 = separationseparation
    while True:
        dy = (0.5dymin) + (0.5dymax)
        dx = sqrt(1.0 - dydy)
        new_x = x + dxstep
        new_y = y + dystep
        if dy == dymin or dy == dymax:
            return new_x, new_y
    s2 = (new_x - other_x)*(new_x - other_x) + (new_y - other_y) * (new_y - other_y)
    if s2 < d2:
        dymin = dy
    elif s2 > d2:
        dymax = dy
    else:
        return new_x, new_y


Actual fit is r=1.53031696, x0=4.346895, y0 = 4.469692
def sample(out, x, y, other_x, other_y, d, note=None):
    global fit_r, fit_x0, fit_y0, fit_min, fit_max
    r = sqrt((x - other_x)(x - other_x) + (y - other_y)(y - other_y))
    out.write("%9.6f   %9.6f %9.6f   %9.6f %9.6f   %9.6f" % (d, x, y, other_x, other_y, r))
    if x >= fit_x0 - fit_r and x <= fit_x0 + fit_r:
        fit_dy = fit_y0 - y + sqrt(fit_rfit_r - (x - fit_x0)(x - fit_x0))
        fit_min = min(fit_min, fit_dy)
        fit_max = max(fit_max, fit_dy)
        out.write("   %+9.6f" % (fit_dy))
    if note is not None:
        out.write("   %s" % note)
    out.write("\n")
if name == 'main':
    from sys import stdout, stderr
stderr.write(&quot;Length Our_x Our_y Other_x Other_y Separation\n&quot;)
fit_x0  = 4.352082
fit_y0  = 4.460968
fit_r   = 1.539033
fit_min = 6
fit_max = 0
x = 3
y = 3*sqrt(3)
d = 6.0         # sqrt(3^2 + (3*sqrt(3))^2) = sqrt(9 + 9*3) = sqrt(36) = 6 
R = 6.0
s = 1.0/(12*64) # 1/64th of an inch

sample(stdout, 0, 0, *other(0), 0, &quot;Initial&quot;)
sample(stdout, x, y, *other(d), d, &quot;First contact&quot;)

# Avoid
while True:
    other_x, other_y = other(d + s)
    next_x, next_y = avoid(x, y, other_x, other_y, R, s)
    if next_x &lt;= other_x:
        x, y, d = next_x, next_y, d + s
    else:
        smin = 0
        smax = s
        while True:
            smid = smin + 0.5*(smax - smin)
            other_x, other_y = other(d + smid)
            next_x, next_y = avoid(x, y, other_x, other_y, R, smid)
            if next_x &lt; other_x:
                smin = smid
            elif next_x &gt; other_x:
                smax = smid
            else:
                break
        x, y, d = next_x, next_y, d + smid

    if next_x &gt;= other_x:
        sample(stdout, x, y, other_x, other_y, d, &quot;Peak&quot;)
        break
    else:
        sample(stdout, x, y, other_x, other_y, d)

# Veer back
while True:
    other_x, other_y = other(d + s)
    next_x, next_y = avoid(x, y, other_x, other_y, R, s)

    # Do not overcorrect from target
    if (next_x * y - next_y * x) &lt;= 12.0 * (y - next_y):
        break

    x, y, d = next_x, next_y, d + s
    sample(stdout, x, y, other_x, other_y, d)

# Final line segment
next_x = 12
next_y = 0
d += sqrt((next_x - x)*(next_x - x) + (next_y - y)*(next_y - y))
sample(stdout, next_x, next_y, *other(d), d)

stderr.write(&quot;Done.  Total path length is %.6f and circular fit y difference was %+.6f to %+.6f\n&quot; % (d, fit_min, fit_max))

By taking the curved path instead of the polyline, one saves a whopping $0.188\text{ ft}$, or approximately two and a quarter inches.

Answer 4

Person A starts at point A and has to keep minimum of $6$ ft. distance from person B. Person B starts from point B and walks straight to point A. Both A and B have same speed.

Please see the diagram below. Path taken by person A is AD, DE and EB to get to point B.

$AC = 6, AD = 4 \sqrt3$.

He then walks distance $DE$ parallel to line $AB$ and point $E$ is such that $\angle CM'E = 60^0$ and $EM' = CD = 4 \sqrt3 - 6$.

So, $DE = CM' - (CD+EM').cos60^0 = 3 - (4 \sqrt3 - 6) = 9-4\sqrt3$.

Please note $AD + DE = 9$, so when person A is at point E, person B has already reached $C'$. So they have vertically crossed each other safely somewhere between point $D$ and $E$. Please also note that $C'M' = 6.$

This makes it safe for person A to now go straight from E to B.

$EE' = EM'.cos60^0 = 2 \sqrt3 - 3, EB' = 6 + EE' = 3 + 2 \sqrt3$

$BE = \sqrt{BB'^2+EB'^2} \approx 8.82$, and as obtained above, $AD + DE = 9$

So, total distance traveled by person A to reach point B keeping 6 ft. of min. distance from person B $\approx 17.82$.