8

The braid groups satisfy a number of properties that one would expect of a hyperbolic group, liking having a solvable word problem, and having exponential growth. Are the braid groups hyperbolic groups? If not, is there any obvious property of hyperbolic groups showing that they are not?

Quizzical
  • 394
  • 5
    Most braid groups contain a $\mathbb{Z}\times\mathbb{Z}$ subgroup... – Steve D Jul 30 '20 at 23:52
  • More specifically, if I'm understanding correctly, even $B_3$ (which doesn't immediately have such a subgroup) shouldn't be hyperbolic because of the Euclidean subgroups of the modular group $SL(2,\mathbb{Z})$. – Steven Stadnicki Jul 30 '20 at 23:56
  • 1
    @StevenStadnicki I don't know what you mean by "Euclidean subgroup of $SL_2(Z)$"... indeed $SL_2(Z)$ is hyperbolic. Nevertheless, $B_3$ has an infinite center and contains copies of $Z^2$ (it is virtually direct product $\mathbf{Z}$ $\times$ free). – YCor Aug 04 '20 at 15:45

1 Answers1

11

Outside of the one and two strand case they are not hyperbolic. One obstruction is that braid groups on $n>2$ strands, $B_n$, contain $\mathbb Z^2$ subgroups which can not happen in hyperbolic groups.

First note that $B_3$ is a subgroup of $B_n$ for $n>2$. Order the strands and name them $b_1,b_2,b_3,...,b_n$. Let $\sigma$ be the element which braids $b_1$ around $b_2,b_3$ where $b_1$ goes around the back of those two and then cross in front and let $\rho$ be the element which braids $b_2,b_3$ (basically an element in $B_2$). These two elements "obviously" commute so we get $\langle \sigma, \rho \rangle \cong \mathbb{Z}^2$ as a subgroup of $B_n$ for $n>2$ (if you want a formal proof there is enough detail in A Primer on Mapping Class Groups by Farb and Margalit). 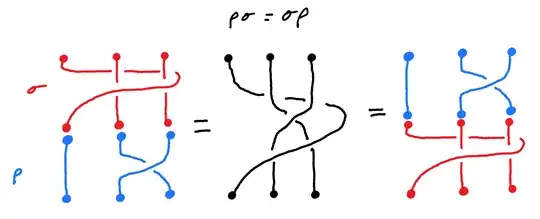enter image description here In the case of $B_1,B_2$ we have the trivial group and $\mathbb{Z}$ respectively and these are hyperbolic but not in an "interesting" way.

You mention that one of your motivations is that there do seems to be some similarities to hyperbolic groups and it turns out this is a really good observation which gets into some interesting math. I won't be giving much details but it seems good to mention some of these ideas.

There is a different way to describe braid groups and it is as mapping class groups of punctured disk (basically the group of topological symmetries up to a natural identification). Very roughly you can think about punctures moving around each other in the disk as braids moving around each other. If you "plot" this with a time axis you can see the punctures moving "drawing" the braid.

This becomes important because now you get tools from surface theory and their mapping class groups. The mapping class group acts naturally on something called the curve complex which, somewhat surprisingly, is $\delta$-hyperbolic, proved by Masur and Minsky, and infinite diameter (you can choose $\delta =19$). Lots of the hyperbolic behavior can actually be seen in this action on the curve complex. Further, Masur and Minsky developed a way of studying the geometry of mapping class groups through the curve complex of the surface and curve complexes of all its (essential) subsurfaces by "piecing together" the geometric information of the curve complexes in some consistent way.

  • 1
    Possibly worth noting in addition to this: $\rho^2$ also commutes with $\sigma$ and $\langle\sigma, \rho^2\rangle$ is still isomorphic to $\mathbb{Z}^2$. Since $\sigma$ and $\rho^2$ are both in the pure braid group, that group also isn't hyperbolic. – Steven Stadnicki Jul 31 '20 at 00:25
  • 2
    @StevenStadnicki Yes, that is a way to get it to work with the pure braid group. Another way to tell is that the pure braid group is finite index in $B_n$ since it is the kernel of the natural map to $S_n$. –  Jul 31 '20 at 00:29
  • I say $\delta =19$ for the hyperbolicity constant but the paper I cite says you can do $\delta=17$. I remember going through the paper years ago and not able to figure out how they got $17$ but I could get $19$, but I could have very easily been missing something. In either case $19$ works and I don't think people believe that $17$ is sharp anyways. –  Jul 31 '20 at 01:31
  • Another part of this story is acylindrical hyperbolicity which is a big generalization of hyperbolic groups while still having lots of the tools. These groups are not acylindrically hyperbolic, but closely related groups, mapping class group of sphere with punctures, are acylindrically hyperbolic –  Jul 31 '20 at 02:21