2

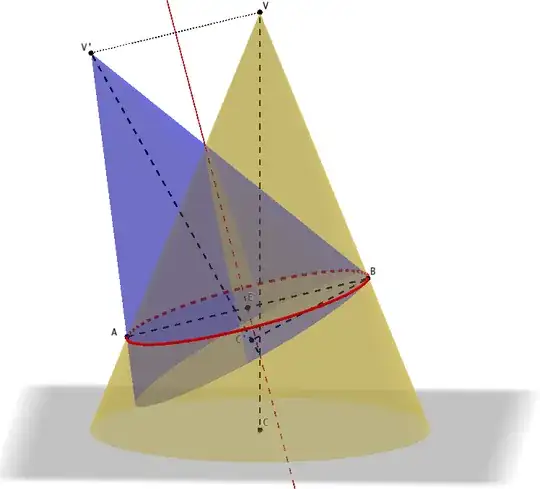
I am trying to model the join of the leading edge of this 'wing'.

https://www.kites-and-more.com/images/duotone-wing-foil-p628-6241_medium.jpg

The tubes are inflated, each section is conical in shape. I know the radius of the tubes at each joint. Given a vector in 3D space of each joint, the radius of the tube, the direction of the tube (another vector) how can I model the joint?

I am coding this in Python.

My thoughts are:

  • If these were tubes, a cross section of the join would be an ellipse
  • I don't know how to angle the ellipse (see the picture) if the tubes are NOT on the same plane
  • I don't know how to approach the joint if the tubes taper
  • tubes will share ellipse focus points

https://www.mackiteboarding.com/product_images/uploaded_images/north-rebel-kite-2013.jpg

Intelligenti pauca
  • 55,765
user3719901
  • 23
  • I've just posted a partial answer, but to be more specific you should explain some details. In particular, what do you mean by "I know the radius of the tubes at each joint"? If the joint is not perpendicular to the axis, you cannot have a single radius. – Intelligenti pauca Jul 19 '20 at 14:43
  • You're asking the interesting questions! I'm not 100% sure what other bits of software do. Usually the tube is defined as a percentage of the profile length, as the tube becomes part of the profile. So the profile changes length, so the tube diameter changes. – user3719901 Jul 26 '20 at 22:15
  • I think the known radius is the minor axis - I want to stretch the tube at the corner. What I need is the major axis, the angle and a way to draw the ellipse in the correct location – user3719901 Jul 26 '20 at 22:27
  • It is not at all clear what you exactly want to do: without a detailed information it's impossible to help you. If you are given a single long frustum that you must cut into smaller pieces and reassemble them to make a curved tube, then my answer below gives all the info you need: just cut at half the angle between the axes and rotate the upper part of 180°. If that is not the case you should explain IN A DETAILED WAY what you need. – Intelligenti pauca Jul 27 '20 at 07:43
  • The answer you gave, I'm sure is very good and gave me a lot of ideas, but your cones end in points. As you can see in the photos, the tubes do not end in points. So I don't know how to construct what I see in the photos. I am very very thankful for your answer as it gave me insight into the problem. – user3719901 Jul 28 '20 at 12:14
  • What I ended up doing was creating two 3D vectors that share one point. I created a plane through that joint, angle 'e' in your diagram. I then used the known radius to project a circle from the end of the vector to the plane, thus achieving the ellipse. Then, with the smaller radius, did the same thing, but on the other end of the vector. These two ellipses seem to be the ends of the cone. It looks ok. Not 100% sure yet. – user3719901 Jul 28 '20 at 12:18
  • Your diagram was interesting, but cutting the cones out of cloth and sewing them would not end up with a kite shaped item. Maybe V' needs to be where C is? I don't know. (lots of comments - the five minute limit is hurting me :) ) – user3719901 Jul 28 '20 at 12:21
  • But thank you, again. It really helped! – user3719901 Jul 28 '20 at 12:22
  • Glad I was of help: I drew cones instead of frustums because the software I've used doesn't give an easy way to draw them. I don't understand your comment about "cutting the cones out of cloth and sewing them": of course I represented a single joint, to complete the kite you must go on and insert the others to form a curved tube; two such tubes, joined together, will give the final result. – Intelligenti pauca Jul 28 '20 at 13:10
  • If you mean you want to make the lateral surface of a cut frustum by cutting a piece of cloth, then be warned that the cut is not linear but has a complicated shape: http://www.matematicasvisuales.com/english/html/geometry/planenets/coneobliq.html – Intelligenti pauca Jul 28 '20 at 13:19

1 Answers1

1

The intersection between two cones is, in general, very complicated. But the intersection between a cone and a plane is an ellipse (if the inclination of the plane is small, as in the case at hand) and it is not difficult to construct two cones having a given elliptical section in common (see the details here, for instance).

If, in particular, the cones have the same aperture the construction is very easy (see figure below). Suppose the first cone has vertex V and is cut by a plane $\alpha$, the intersection being an ellipse of major axis $AB$. Consider the line perpendicular to the plane and passing through the center $E$ of the ellipse and let $V'$ be the reflection of $V$ about this line: a second cone, with the same aperture as the first one, vertex $V'$ and axis the bisector of $AV'B$, will also intersect plane $\alpha$ in the same ellipse. The angle between the axes is twice the inclination of plane $\alpha$ with respect to the base of the first cone.

enter image description here

Intelligenti pauca
  • 55,765