Consider the following Langevin equation $$\frac{d^2 x}{dt^2}+\omega_n^2x=\eta(t),$$ where $\eta(t)$ has a gaussian probability distribution with mean zero and correlation $$\langle \eta(t) \eta(t')\rangle = D\delta(t-t'),$$ where $\delta(t-t')$ is the dirac delta function. In this post they show that the solution is $$\langle x(t) \rangle = 0$$ $$\langle x^2(t) \rangle = \frac{D}{2\omega_n^3}[\omega_n t - \sin(\omega_n t) \cos(\omega_n t)].$$
I want to confirm this result using a Fourier series method.
Let
$$\eta(t) = a_0 X_0 + \sum_{k=1}^\infty a_k X_k \cos(\omega_k t) + b_k Y_k \sin(\omega_k t),$$
where $X_k$, $Y_k$ are independent random gaussian variables with mean 0 and variance 1. By solving the differential equation for a sinusoidal driver we get
$$x(t) = \sum_{k=0}^\infty x_k(t),$$
where
$$x_k(t) = \begin{cases}
\frac{a_k X_k\omega_n[\cos(\omega_n t) - \cos(\omega_k t)] + b_k Y_k[\omega_k\sin(\omega_n t) - \omega_n\sin(\omega_k t)]}{\omega_n(\omega_k^2 - \omega_n^2)}, & \omega_k \ne \omega_n \\
\frac{a_k X_k\omega_n t \sin(\omega_n t) + b_k Y_k[\sin(\omega_n t) - \omega_n t \cos(\omega_n t)]}{2\omega_n^2}, & \omega_k = \omega_n.
\end{cases}$$
Therefore, the soltion should be given by
$$\langle x(t) \rangle = 0,$$
$$\langle x(t)^2 \rangle = \sum_{k=0}^\infty\langle x_k(t)^2 \rangle,$$
where
$$\langle x_k^2(t) \rangle = \begin{cases}
\frac{a_k^2\omega_n^2[\cos(\omega_n t) - \cos(\omega_k t)]^2 + b_k^2[\omega_k\sin(\omega_n t) - \omega_n\sin(\omega_k t)]^2}{\omega_n^2(\omega_k^2 - \omega_n^2)^2}, & \omega_k \ne \omega_n \\
\frac{a_k^2\omega_n^2 t^2 \sin^2(\omega_n t) + b_k^2[\sin(\omega_n t) - \omega_n t \cos(\omega_n t)]^2}{4\omega_n^4}, & \omega_k = \omega_n.
\end{cases}$$
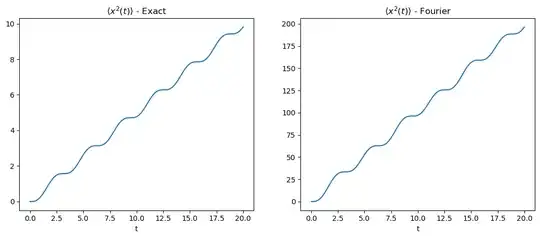
Therefore, letting $a_k=b_k=D$, shouldn't the formulas for the variances agree? I tried to confirm this in python but they are not the same. Here is the code and outputted figures:
import numpy as np
import matplotlib.pyplot as plt
def white_noise(t):
eta = a[0] * np.random.normal()
for k in range(1,N+1):
eta += a[k] * np.random.normal() * np.cos(omega[k] * t)
eta += b[k] * np.random.normal() * np.sin(omega[k] * t)
return eta
def variance_exact(t):
return D / 2 / omega_n ** 3 * (omega_n * t - np.sin(omega_n * t) * np.cos(omega_n * t))
def variance_fourier(t):
var_for = variance_fourier_term1(t, 0)
for k in range(1,N+1):
if omega[k] != omega_n:
var_for += variance_fourier_term1(t, k)
elif omega[k] == omega_n:
var_for += variance_fourier_term2(t, k)
return var_for
def variance_fourier_term1(t, k):
term1 = a[k] ** 2 * omega_n ** 2 * (np.cos(omega_n * t) - np.cos(omega[k] * t)) ** 2
term1 += b[k] ** 2 * (omega[k] * np.sin(omega_n * t) - omega_n * np.sin(omega[k] * t)) ** 2
term1 = term1 / omega_n ** 2 / (omega[k] ** 2 - omega_n ** 2) ** 2
return term1
def variance_fourier_term2(t, k):
term2 = a[k] ** 2 * omega_n ** 2 * t ** 2 * np.sin(omega_n * t) ** 2
term2 += b[k] ** 2 * (np.sin(omega_n * t) - omega_n * t * np.cos(omega_n * t)) ** 2
term2 = term2 / 4 / omega_n ** 4
return term2
P = 20
N = 1000
k_array = np.arange(N+1)
omega = np.pi * k_array / (2 * P)
omega_n = 1
D = 1
t_min = 0
t_max = P
nt = 1024
t = np.linspace(t_min, t_max, nt)
a = np.full(N+1, D)
b = np.full(N+1, D)
b[0] = 0
fig = plt.figure()
fig_size = fig.get_size_inches()
fig_size[0] = 2 * fig_size[0]
fig.set_size_inches(fig_size)
ax = fig.add_subplot(121)
ax.plot(t, variance_exact(t))
ax.set_xlabel('t')
ax.set_title(r'$\langle x^2(t)\rangle$ - Exact')
ax = fig.add_subplot(122)
ax.plot(t, variance_fourier(t))
ax.set_xlabel('t')
ax.set_title(r'$\langle x^2(t)\rangle$ - Fourier')
fig.savefig('temp_figures/variance_exact_vs_fourier.png', bbox_inches = 'tight')
plt.show(block = False)
Edit: Fixed bug on line 25 of code.