5

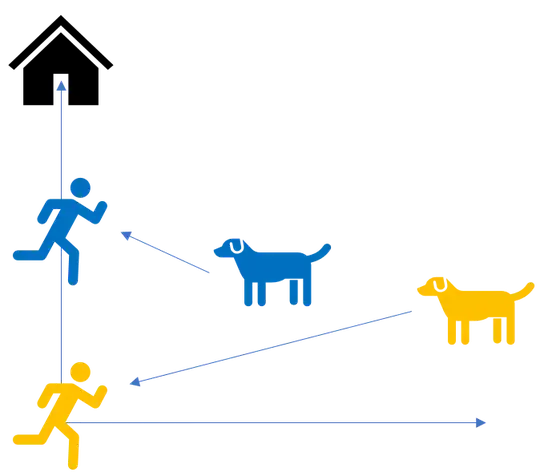
When walking yesterday I stumbled upon one of these humorous1 signs "my dog runs from the gate to the door in 4 seconds, if you are slower stay where you are". This made me think about the general problem

enter image description here

The unfortunate guest starts running at the orange position with speed $v_\textrm{h}$, as does the dog. The dog always runs directly towards the guest with a speed $v_\textrm{d}$. The blue color shows the situation after some time.

$v_\textrm{h}$ and $v_\textrm{d}$ are constant.

I am curious about the shape of the dog's path.

Being nowadays better with computer than with math, I will simulate this experiment2 but would like to understand whether there is hope for a formal mathematical solution - and how to get there (even pointing to the general direction would be wonderful). It would be a great test before diving into the second footnote.

Now that I think about it, it should be similar to the path of a swimmer in a river who swims directly towards the bank

1 The level of humour depends on the size of the dog.

2 I will also simulate the problem where $v$ is a function of time. I started to think about some realistic functions such as $v_\textrm{h}(t) = \alpha te^{-\beta t}$ (you start fast, then get tired) or a velocity that is a function of the distance between the protagonists. I believe that this is too complicated for a formal solution.

WoJ
  • 836
  • 1
    That would be the aptly name "dog curve" https://en.wikipedia.org/wiki/Radiodrome. – Raoul Jul 14 '20 at 18:32
  • 1
    You might look up radiodrome – Robert Israel Jul 14 '20 at 18:32
  • Let me ask another question: assuming that it's a lawn between the gate and the door of the house, do you think the guest can have a better strategy than running straight toward the door? What will then be the path of the guest, and the path of the dog? And what will be the minimal speed of the guest to be able to reach the door? – WhatsUp Jul 14 '20 at 18:33
  • 1
    Duplicate of https://math.stackexchange.com/q/244333/42969? – Martin R Jul 14 '20 at 18:47
  • @MartinR: oh yes it is, thank you. I will mark it as duplicate but will be back with an edit of my question once I simulated the other velocities. – WoJ Jul 14 '20 at 18:50
  • @Raoul: thank you – WoJ Jul 14 '20 at 18:50
  • @RobertIsrael: thank you – WoJ Jul 14 '20 at 18:50

0 Answers0