3

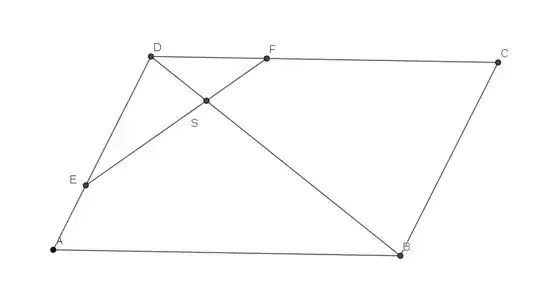
Let $ABCD$ be a parallelogram and let $E\in\overline{AD},\ F\in\overline{CD}$ such that: $$\frac{|AE|}{|ED|}=\frac{|DF|}{|FC|}=\frac12.$$ Find the ratio in which the line segment $\overline{EF}$ divides the diagonal $\overline{BD}$.

One approach I'm familiar with:

$\overrightarrow{AB}=\overrightarrow{DC}\ \&\ \overrightarrow{AD}=\overrightarrow{BC}$

Let $S$ be the intersection point of $\overline{EF}$ and diagonal $\overline{BD}$, then:

$\overrightarrow{ES}=\lambda\overrightarrow{EF}\ \&\ \overrightarrow{DS}=\mu\overrightarrow{DB}$

$\overrightarrow{ES}=\lambda\overrightarrow{EF}=\lambda\left(\overrightarrow{ED}+\overrightarrow{DF}\right)=\lambda\left(\frac23\overrightarrow{AD}+\frac13\overrightarrow{DC}\right)=\frac{2\lambda}3\overrightarrow{AD}+\frac{\lambda}3\overrightarrow{AB}$

On the other hand,

$\overrightarrow{ES}=\overrightarrow{ED}+\overrightarrow{DS}=\frac23\overrightarrow{AD}+\mu\overrightarrow{DB}=\frac23\overrightarrow{AD}+\mu\left(\overrightarrow{DA}+\overrightarrow{AB}\right)=\left(\frac23-\mu\right)\overrightarrow{AD}+\mu\overrightarrow{AB}$

$\overrightarrow{AD}$ and $\overrightarrow{AB}$ can form a basis, so we have obtain the following system:

$$\begin{cases}\frac{2\lambda}3&=\frac23-\mu\\\frac{\lambda}3&=\mu\end{cases}\implies \lambda=\frac23\implies\mu=\frac29$$

So we get that $\overline{EF}$ divides the diagonal $\overline{BD}$ in the ratio $2:7$

My question:

How can we solve this problem using the following theorem about the composition of two homotheties ( found here, in the answer by Aqua):

If $\mathcal{H}_{M,k_1}$ and $\mathcal{H}_{N,k_2}$ are homotheties then their compostion $\mathcal{H}_{M,k_1}\circ \mathcal{H}_{N,k_2}$ is again some homothety $\mathcal{H}_{S,k}$ with $k=k_1k_2$ (if $k\ne 1$) and it center $S$ lies on a line $MN$.

I thought I could do the following:

$$\begin{aligned}\mathcal H_{E,-2}&:A\mapsto D\\\mathcal H_{F,-2}&:D\mapsto C\end{aligned}$$ so that the center of the homothety $\mathcal H_{E,-2}\circ\mathcal H_{F,-2}$ lies on the line $EF$, but this doesn't lead me to the right result.

Picture:

enter image description here Thank you very much!

Edit: For future readers, picture according to the answer by @MichaelRozenberg: enter image description here

nonuser
  • 91,557
Matcha Latte
  • 4,665
  • 4
  • 16
  • 49

2 Answers2

2

enter image description here

Let $AB = 6a$. Use similarity (or homothety if you wish): $$ {GA\over DF} = {EA\over ED} ={1\over 2} \implies GA =a$$ so $${DS\over SB} = {DF\over GB} = {2a\over 6a+a} = {2\over 7}$$

nonuser
  • 91,557
1

Let $G\in FC$ such that $AG||EF$, $I\in AB$ such that $CI||AG,$

$AG\cap BD=\{Q\}$, $CI\cap BD=\{R\}$ and $FG=y$.

Thus, $$DF=2y,$$ $$FC=4y,$$ $$GC=3y,$$ $$AI=3y$$ and since $$AB=2y+y+3y=6y,$$ we obtain $$IB=3y,$$ which gives $$QR=RB=3SQ$$ and $$DS=2SQ.$$ Thus, $$\frac{DS}{SB}=\frac{2SQ}{SQ+3SQ+3SQ}=\frac{2}{7}.$$

Michael Rozenberg
  • 203,855