3

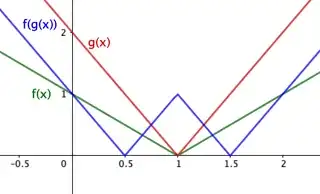
If $f(x)$ and $g(x)$ are differentiable functions at all points in $[a,b]$ except a one point (c) in the interval and continuous everywhere on $[a,b]$. Then it is guaranteed that $f(g(x))$ is differentiable wherever $f$ and $g$ are differentiable but is there an example for which $f(g(x))$ is also differentiable at c . Or can it be proven that something like this can’t happen?

It is true that if they are nowhere differentiable then it is impossible to create an example but is it possible to create an example for such a case?

What about 2 points, 3 points , infinitely many?

Vivaan Daga
  • 6,072
  • The function $g(x)=x^{1/3}$ is not differentiable at $x=0$ but if we let $f(y)=y^3$ then $g\circ f(y)=y$, and this is differentiable everywhere. Does this answer the question? – Giuseppe Negro Jul 03 '20 at 12:30
  • @GiuseppeNegro but $y^3$ is differentiable everywhrere – Vivaan Daga Jul 03 '20 at 12:39
  • I see. What about $g(x)=\lvert x \rvert$ and $$f(y)=\begin{cases} 1, & y\ge 0, \ 0, & y<0?\end{cases}$$ We have that $f\circ g(x)=1$, and both functions are not differentiable at the origin. (Oh, but $f$ is not continuous. Then replace it by $$f(y)=\begin{cases} y, & y\ge 0, \ 0, & y<0.\end{cases}$$ Now it should work) – Giuseppe Negro Jul 03 '20 at 12:51

1 Answers1

3

It is not even guaranteed that $f\circ g$ is differentiable wherever $f$ and $g$ are.

For example, let $f(x) = |x-1|$ and $g(x)=2|x-1|$, which are continuous and differentiable at all points in $[0,2]$ except for $x=1$. But $f(g(x))$ is not differentiable in $x=1/2$ nor $x=3/2$:

enter image description here

The other way around is also possible (example by @Vivaan Daga). Let $f(x)=x^-$ (notation for the negative part of a function) and $g(x)=|x|$. Both are continuous everywhere and differentiable everywhere except in $x=0$. But $f(g(x))=0$ for all $x\in\mathbb{R}$, so $f\circ g$ is differentiable everywhere.

AugSB
  • 5,107