3

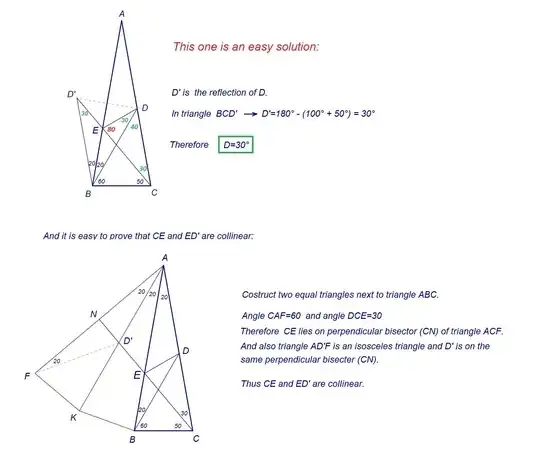
For the well-known problem

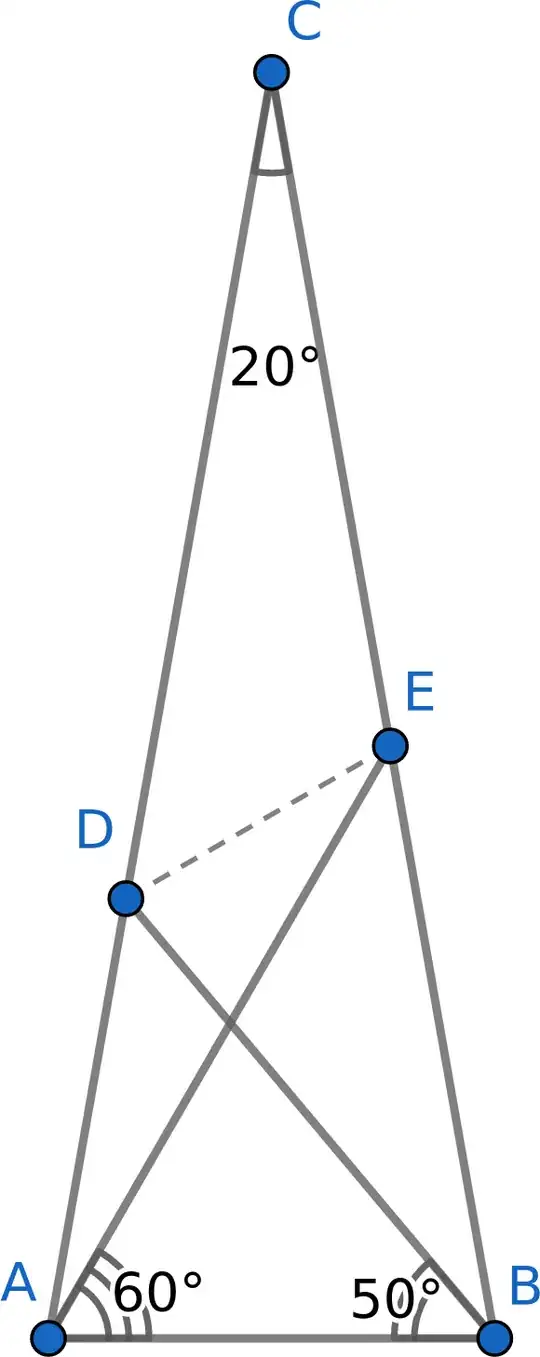
In an isosceles triangle with base $AB$ and $\angle CAB=80^\circ$ taken $D$ on the segment $CA$, $E$ on the segment $CB$ such that $\angle BAE=60^\circ$, $\angle ABD=50^\circ$, find $\angle EDB$.

The question is what is a canonical or otherwise simple without being too artificial way of solving it? Or what was the solution you heard/seen/found first?

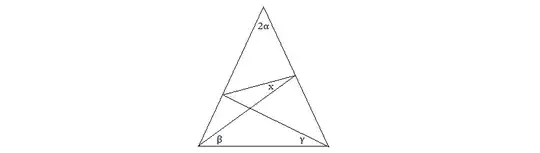
Btw, simple angle chasing does not help. The first way I can think of is considering difference of heights $DH_d$ and $EH_e$ of triangles $ABD$ and $ABE$ respectively along with $H_dH_e$ which together give the inclination angle of $DE$ relative to $AB$ and thus the desired angle. Needed for that lengths of $AD,\,BD,\,AE,\,BE$ can be expressed in terms of $AB$ and known angles by the sine rule. Almost like putting the thing into Cartesian coordinates.

Another approach could be vectors, then taking $A$ or $B$ as the origin makes things more simple, than taking $CA,\,CB$ as basis vectors, IMHO.

By "too artificial" I mean things like this:

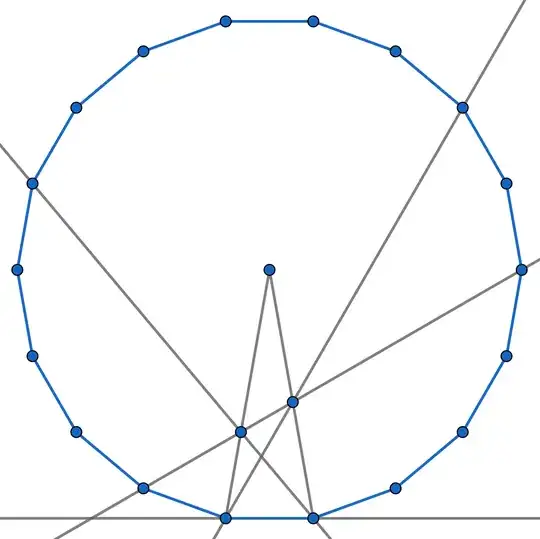
constructing a regular $18$-gon with side $AB$, proving lines $AE,\,BD,\,DE$ contain some diagonals and then finding the angle very easy by angle chasing.

Update:

The solutions are not as trivial as one would expect from the statement. It's called Langley's problem of adventitious angles first posed in The Mathematical Gazette in 1922.
Check out An Intriguing Geometry Problem by Tom Rike.

(from this answer).

Alexey Burdin
  • 5,299
  • So what is the answer? 80 degrees, right? – peter.petrov Jun 30 '20 at 00:38
  • @peter.petrov By the last picture it's easy to see that the angle is half-sum of two subtended arcs of the circumcircle of the $18$-gon, each of them of $4$ chords of $20^\circ$, hence $80^\circ$. Geogebra gives $80^\circ$ too. And the results of algebraical computations simplify to $80^\circ$ too, so I believe yes) – Alexey Burdin Jun 30 '20 at 00:42
  • Draw a line through B parallel to AC. Extend AE and DE until they intersect with the line. Now some very nice things happen. – peter.petrov Jun 30 '20 at 00:46
  • Yeah this leads to a solution. I can write it in detail tomorrow. One gets an isolescent trapezoid and a bunch of similar triangles and several tetragons inscribed in circles – peter.petrov Jun 30 '20 at 01:02
  • No, I got deluded last night. Never mind... I will think some more, it's a nice problem :) – peter.petrov Jun 30 '20 at 08:54
  • Ahh my question appears to be a duplicate... – Alexey Burdin Jun 30 '20 at 09:52

3 Answers3

2

The following solution can be found in Coxeter-Greitzer's book $\textit{Geometry Revisited}$ [Problem $4$ in the last set of exercises in Chapter $1$], one of my favourite books, also I will type out the solution just because it is so beautiful.

Let $EF$, parallel to $AB$, meet $AC$ at $F$. Let $BF$ meet $AE$ at $G$.

$\Delta ABG$ is equilateral $\implies AG = AB$.

$\Delta BAD$ is isosceles $\implies AD = AB$. Hence $\Delta AGD$ is isosceles, $\angle AGD = 80^{\circ}, \ \angle FGD = 40^{\circ}$. Since $\angle DFG = 40^{\circ}$, $\Delta FDG$ is isosceles and $FD=DG$.

Also, $EF = EG \implies \Delta GED \stackrel{\sim}{=} \Delta FED$, $DE$ bisects $\angle FEG$, and $\angle DEA = 30^{\circ} \implies \angle EDB =80^{\circ}$.

A solution I did on my own did not require any constructions, observed a pair or two of similar triangles and used only the sine rule a couple of times along with one useful formula $$\sin(\theta)\sin\left(\theta-\dfrac{\pi}3\right)\sin\left(\theta+\dfrac{\pi}3\right)=\dfrac{\sin{(3\theta)}}4$$

Fawkes4494d3
  • 3,009
1

I think this is a very simple solution: enter image description here

Seyed
  • 9,041
1

enter image description here For an arbitrary isosceles triangle with given angles $\alpha,\> \beta$ and $\gamma$ shown in the graph, the trigonometric solution for the unknown angle $x$ is

$$ \cot x = \frac{ \cos\alpha \cos(\gamma+\alpha)} {\sin\gamma\cos(\beta+\alpha)\cos(\beta-\alpha)}-\tan(\beta-\alpha) $$

(which is derived from the sine rule applied to three triangles.) Then, substitute $\alpha=10$, $\beta= 60$ and $\gamma=50$ into the expression to get

\begin{align} \cot x & = \frac1{\cos 70} -\tan 50 =\frac1{\sin20}-\frac{\cos40}{\sin40}\\ &= \frac{2\cos20-\cos40 }{ \sin40}= \frac{\cos20+\cos80}{ \sin40}\\ &= \frac{2\cos30\cos50}{\sin40}=\sqrt3 \end{align}

Thus, $x=30$ and in turn $\angle EDB = 80$.

Quanto
  • 120,125