Let $f_1(x), f_2(x), \ldots, f_n(x)$ be a set of convex functions. We define $f(x)$ as
$$ f(x) = \underset{i}{\text{max}} \left\{ f_i(x) \right\}. $$
How do I show that $f(x)$ is also convex, and the domain of $f$ is intersection of the domains of $f_i$?
Well, the domain of $f$ must be the intersection of the domains of the constituent functions, otherwise the $\max$ cannot be defined.
More generally, suppose $f_\alpha :C \to \mathbb{R}$ is a family of convex functions, with $\alpha \in A$, some index set, and let $f(x) = \sup_{\alpha \in A} f_{\alpha}(x)$.
Then, for any $\alpha \in A$, $\lambda \in [0,1]$, \begin{eqnarray} f_\alpha(\lambda x + (1-\lambda) y) &\le& \lambda f_\alpha(x) + (1-\lambda) f_\alpha(y) \\ & \le & \sup_{\alpha' \in A} (\lambda f_{\alpha'}(x) + (1-\lambda) f_{\alpha'}(y)) \\ & \le & \sup_{\alpha' \in A} \lambda f_{\alpha'}(x) + (1-\lambda) \sup_{\alpha' \in A}f_{\alpha'}(y) \\ &=& \lambda f(x) + (1-\lambda) f(y) \end{eqnarray}
How taking the supremum of the left hand side gives the desired result: $$f(\lambda x + (1-\lambda) y) \le \lambda f(x) + (1-\lambda) f(y)$$
Alternatively, you could note that $\operatorname{epi} f = \cap_{\alpha \in A} \operatorname{epi} f_\alpha$, and that the intersection of convex sets is convex.
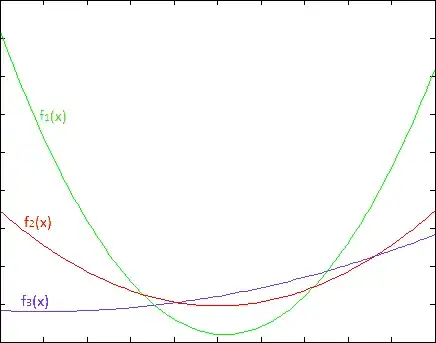
Since it is given that all $f_i(x)$ are convex, we can write the following inequality using Jensen's Inequality.
$$ f_i(\theta x_1 + (1-\theta)x_2) \le \theta f_i(x_1) + (1-\theta)f_i(x_2); \qquad \theta \in [0,1] $$
We take maximum of the both sides.
$$ \underset{i}{\text{max}} \left\{ f_i(\theta x_1 + (1-\theta)x_2) \right\} \le \underset{i}{\text{max}} \left\{ \theta f_i(x_1) + (1-\theta)f_i(x_2) \right\} \qquad \ldots \text{(I)} $$
It is clear that
$$ \underset{i}{\text{max}} \left\{\theta f_i(x_1) + (1-\theta)f_i(x_2) \right\} \le \underset{i}{\text{max}} \left\{\theta f_i(x_1) \right\} + \underset{i}{\text{max}} \left\{(1-\theta)f_i(x_2) \right\}. \qquad \ldots \text{(II)} $$
Substitiute $\text{(II)}$ into $\text{(I)}$:
$$ \underset{i}{\text{max}} \left\{ f_i(\theta x_1 + (1-\theta)x_2) \right\} \le \underset{i}{\text{max}} \left\{\theta f_i(x_1) \right\} + \underset{i}{\text{max}} \left\{(1-\theta)f_i(x_2) \right\} \qquad \ldots \text{(III)} $$
From the definition of $f(x)$ in the OP we can write $\text{(III)}$ as
$$ f(\theta x_1 + (1-\theta)x_2) \le \theta f(x_1) + (1-\theta)f(x_2). \qquad \ldots \text{(IV)} $$
Being able to write $f(x)$ in the form $\text{(IV)}$ implies that it is convex.
Hint: $f_j(t a + (1-t) b) \le t f_j(a) + (1-t) f_j(b)$ for $0 \le t \le 1$. Note that $\max_j (t f_j(a) + (1-t) f_j(b)) \le t \max_j f_j(a) + (1-t) \max_j f_j(b)$...
Another way to do it: $y\geq\max f_i(x)$ iff $y\geq f_i(x)$ for each $i$; so the epigraph of $\max f_i$ is the intersection of the epigraphs of $f_i$, so it is convex, as an intersection of convex is convex. This also shows that the family $f_i$ is arbitrary, ie a $\sup f_i$ is convex whenever the $f_i$s are.
