The assertion works not just for a parabola but for any conic. From your comment, I assume that a projective explanation is what you want. You need two background lemmas.
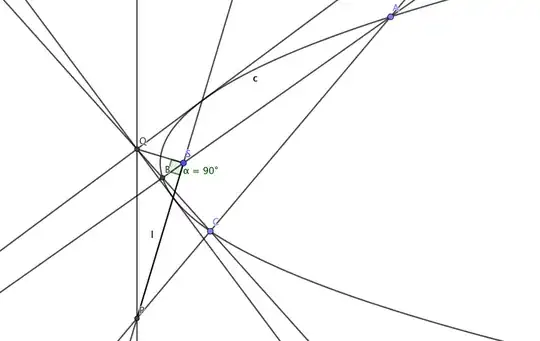
Lemma 1: conjugate points on the directrix of a conic subtend an angle of $90 ^{\circ}$ at the focus.
(In fact the focus can be defined projectively as the point through which conjugate lines are perpendicular.)
Lemma 2: For a conic $c$, a line $s$, its pole $S$, a point $C$ on $c$, and a chord $AB$ that passes through $S$, the points $P,Q$ of intersection of the lines $CA$ and $CB$ with $s$ are conjugate.
If $s$ and $S$ are a directrix and its corresponding focus, then Lemma 2 says the points $P$ and $Q$ are conjugate, and Lemma 1 says they subtend a $90^{\circ}$ angle at $S$.
As for the lemmas, background, terminology and proofs can be found in Hatton's Projective Geometry, 1913. For Lemma 1, see pg 175. For Lemma 2, see pg 133. (Although the construction given on pg 133 is for the case of a circle, it can be used for any conic, and the proof works for any conic. Even if the proof used a special property of the circle, a circle can be projectively transformed into any conic and vice versa, which would prove the lemma for any conic. See also Article 97 on pg 179)