2

And the catch is the first die has $x$ sides, while the second die has $y$ sides, where $x\neq y$

I had this figured out several years ago, but apparently have forgotten both the answer and too much math since then to either work it out or figure it out from Googling.

Similar questions have been asked before, but all the answers are simplified to two dice with the same number of sides on the symmetry that $P(A>B) = P(B>A)$, which does not hold true for my case. What I need to know is:

Given two discrete, uniform distributions, what is the probability that a sample from the first is strictly greater than a sample from the second?

Given $X$ distributed uniformly in $\lbrace0,1,2,3,...,x\rbrace$ and
Given $Y$ distributed uniformly in $\lbrace0,1,2,3,...,y\rbrace$

How can I find $P(X>Y)$?

Community
  • 1
Darth Android
  • 123

1 Answers1

7

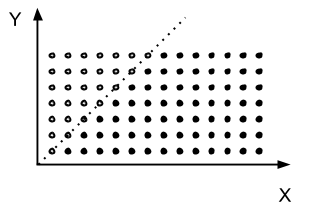
enter image description here

Let these dots be the points $\{(x,y): x\in X, y\in Y\}$. What is the ratio of number of points under the line $y = x$ marked black against the total number of points? This picture is for $x\ge y$. How does the picture look when $y\ge x$?

Alternatively by law of total probability

If we assume $x\ge y$, then $$P(X>Y) = \sum_{j = 1}^y P(X>j)P(Y = j) = \sum_{j = 1}^y\frac{x-j}{x}\cdot \frac{1}{y} =\frac{1}{xy}(xy-\frac{y(y+1)}{2}) $$

I intentionally didn't simplify the last expression, because $(xy-\frac{y(y+1)}{2})$ is the total number of black points, and we divide by total number of points $xy$. Now you can see the connection between probability method and geometric meaning.

Now for the case $y\ge x$, we have $$P(X>Y) = \sum_{j = 1}^x P(X>j)P(Y = j)$$ I encourage you to work this out and draw a picture.

[EDIT]
As discussed in the comments, $$P(X>Y) = \sum_{j = 1}^{\max(x,y)} P(X>j)P(Y = j) = \sum_{j = 1}^{\min(x,y)} P(X>j)P(Y = j) $$ because when $j$ goes beyond $\min(x,y)$ then either $P(X>j) = 0$ or $P(Y = j) = 0$. Also this can be verified from picture as well.

mez
  • 10,887
  • 5
  • 55
  • 109
  • 1
    Great picture...clear and concise! – Eleven-Eleven Apr 25 '13 at 20:42
  • The graph visualization helps considerably! Still trying to figure out how to reconcile the two cases together - as a programmer my mind keeps jumping to min(x,y) or an if/then case, but I desire a simple $f(x,y)$. I can see that the summation fails to work for both cases when $j$ ends up going greater than $x$. I'm afraid I don't have any good graph paper here, but I plan to figure this out when I get home and am not expected to be working on other things. – Darth Android Apr 25 '13 at 21:15
  • Does $P(X>j) \neq \frac{x-j}{x}$ ? I imagine that $P(X>j) = 0$ when $j > x$, but $\frac{x-j}{x} < 0$ when $j > x$. I imagine this is where the "assume $x \geq y$" comes into play... – Darth Android Apr 25 '13 at 21:18
  • @DarthAndroid You are right. The formula is $P(X>Y) = \sum_{j = 1}^{\max(x,y)} P(X>j)P(Y = j)$ for both cases. But in the case of $y\ge x$, there is no need to sum up to $\max(x,y)$, summing up to $x$ (in fact $x-1$) is enough. Because beyond that $P(X>j) = 0$, so we are summing up zeros after j reaches $x-1$. And before that point it is true that $P(X>j) = (x-j)/x$. Likewise when $x\ge y$ we sum till $y$ because beyond that point $P(Y = j) = 0$. This is why when $x\ge y$ we sum till $y$ and when $x\le y$ we sum till $x$. – mez Apr 25 '13 at 21:23
  • @DarthAndroid So essentially I am say that sum up till $\min(x,y)$, after that point summands are $0$ anyway. – mez Apr 25 '13 at 21:29