5

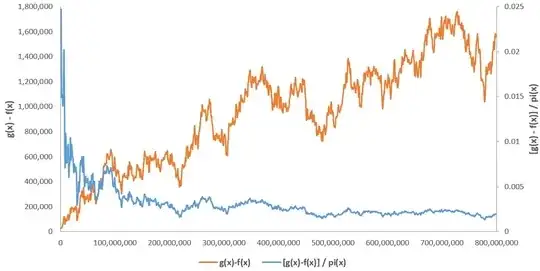
I wanted to see if the numbers preceding primes behaved differently in any way form the numbers succeeding primes so I calculated at the average number of divisors of number of the form $p-1$ and $p+1$ where $p$ is a prime.

Let $d(n)$ be the number of divisors of $n$. Define $f(x) = \sum_{p \le x} d(p-1)$ and $g(x) = \sum_{p \le x} d(p+1)$ where $p$ is a prime. I observed that there are only $3251$ instances where $f(x) < g(x)$. The largest value of $x$ for which this is true is $x = 3752789$. After checking till $x \le 1.9 \times 10^{10}$, I could not find the inequality reversing again.

This the data shows that the numbers preceding primes have on a average fewer number of divisors than the numbers succeeding primes. The graph below shows the actual data.

Question: Is there any reason why this should be true?

enter image description here

Source code

import numpy
p = 2
i = fd = fp = 0
d1 = d2 = p1 = p2 = 0
target = step = 10^6

while True:
    i  = i + 1

    d1 = d1 + len(divisors(p-1))
    d2 = d2 + len(divisors(p+1))
    if d1 > d2:
        fd = fd + 1


p1 = p1 + len(prime_factors(p-1))
p2 = p2 + len(prime_factors(p+1))
if p1 &gt; p2:
    fp = fp + 1

if i &gt; target:
    print i,p,d1,d2,fd, d2-d1,(d2-d1)/i.n(), p1,p2,fp, p2-p1
    target = target + step

p = next_prime(p)
Nilotpal Sinha
  • 24,086
  • 1
    Interesting. Is the difference significant? I mean...what does $|f(x)-g(x)|$ look like? Or $\frac {f(x)}{g(x)}$. – lulu Jun 16 '20 at 21:03
  • 1
    reminds me of this similar but different question – J. W. Tanner Jun 16 '20 at 21:04
  • 1
    One possible reason, but I haven't investigated how significant it can be, is that, at least for smaller primes, the primes modulo $3$ have more congruent to $2$ than $1$ (e.g., see the answer to MO's Consecutive Primes mod 3) and the primes modulo $4$ have more congruent to $3$ than $1$ (e.g., see the answer to MO's A "bit" of primes). This similar issue appears to also be the case for some other modulos, at least for smaller primes. – John Omielan Jun 16 '20 at 21:07
  • 1
    Related to my comment above, I only skimmed through the paper, but it seems the first part of it which you can access from arXiv at Prime Number Races has some possible useful information for you. For example, near the bottom of page #$5$, it says the # of primes less than $x$ of the form $3n + 1$ out-number those of $3n + 2$ first only at $x = 608\text{,}981\text{,}813\text{,}029$. – John Omielan Jun 16 '20 at 21:29
  • 2
    $\sum_{3k \le x} d(3k)=5/9(x\log x)+O(x)$ while the others (on $3k \pm 1$) are $(2/9)x\log x +O(x)$ each, so it is a $5/2$ ratio in the main term- I expect the fact that $3n+2$ wins the prime race so much oftener and $3n+3$ succeeds it, explains the data; proving it though may be quite hard – Conrad Jun 17 '20 at 00:20
  • @lulu $g(x)-f(x)$ fluctuates. For the first $3.9 \times 10^6$ primes it is $325774$. For the first $9.2 \times 10^6$ primes it is $654997$. For the first $11.2 \times 10^7$ it is $302853$. My code is running. It will be interesting to see if it drops below zero for some large value of $x$. – Nilotpal Sinha Jun 17 '20 at 04:56
  • 1
    One reason might be that bigger numbers tend to have more divisors than smaller numbers ($p+1>p-1$). – John Bentin Jun 17 '20 at 08:25
  • @lulu Added a graph which quantifies how large or significant the difference is – Nilotpal Sinha Jun 18 '20 at 05:14
  • @JohnBentin Based on your comment, I did some computation. I don't think that being bigger is the only reason because data shows that the proportion of integer pairs $n,n+2$ such that $d(n) > d(n+2)$ is equal to the proportion of integer pairs $n,n+2$ such that $d(n) < d(n+2)$. If bigger was the sole reason then the proportion of $d(n) < d(n+2)$ should have been detectably greater – Nilotpal Sinha Jun 18 '20 at 14:38

1 Answers1

3

Too long for a comment,

For $a=\pm 1$ $$\sum_p d(p -a)p^{-s}=\sum_{k\ge 1} \sum_{lk+a \ prime} (lk+a)^{-s}=\sum_{k\ge 1} \sum_{\chi\bmod k} \frac{\chi(a)}{\varphi(k)}\sum_p \chi(p)p^{-s}$$

$$\sum_p (d(p-1)-d(p+1))p^{-s}=\sum_k \sum_{\chi\bmod k} \frac{1-\chi(-1)}{\varphi(k)}\sum_p \chi(p)p^{-s}$$

Under the GRH each term is analytic for $\Re(s) > 1/2$,

If $\chi^2$ is a non-trivial character then $\sum_p \chi(p)p^{-s}$ is analytic at $s=1/2$, if $\chi$ is a quadratic character then as $s\to 1/2^+$ $$\sum_p \chi(p)p^{-s}=\sum_{m\ge 1}\frac{\mu(m)}{m}\log L(sm,\chi^m)\sim \frac{1}2\log(s-1/2)$$

thus $$\lim_{s\to 1/2^+}\frac{ \frac{1-\chi(-1)}{\varphi(k)}\sum_p \chi(p)p^{-s}}{\log(s-1/2)} =\frac{1_{\chi \text{ is a quadratic odd character}}}{\varphi(k)}$$ Is this not too bad to conjecture that ? $$\lim_{s\to 1/2^+}\sum_p (d(p-1)-d(p+1))p^{-s}=\color{red}{-\infty}$$ Estimating the growth of $\sum_{p\le x} d(p-1)-d(p+1)$ thus the abscissa of convergence of the Dirichlet series would help.

reuns
  • 79,880