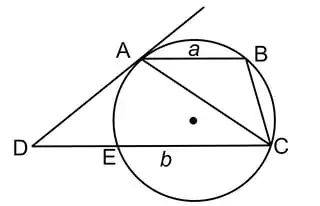
Geometry problem I am having trouble to solve

Question

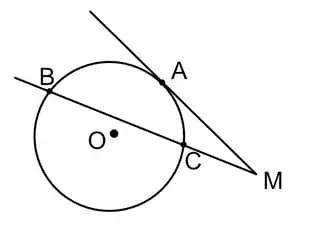
Prove that $AC = \sqrt{ab}$

$a$ is $AB$; $b$ is $CD$; the dot is the origin of the circle. ABCD is a trapezoid, meaning AB || DC.

My attempt at solving:

According to this rule,

$$MA^2 = MB \cdot MC$$

I can apply this rule and say that $DA^2 = b\cdot DE$. If I manage to prove that $DE = a$, I solve the problem, because if $DE = a$, that means that $DA = BE$, which leads to $BE = AC$, because both are diagonal of the equilateral trapezoid (ABCE) in the circle.

You don't have enough information. 1) you can move the point $B$ about and thus change $a$ but keep $AC$ and $b$ the same so $\sqrt{ab}$ can be changed to many values but $AC$ will stay what it is. 2) Is the circle a unit circle? — fleablood, Jun 16 '20 at 20:49
we do know that AB ∥ CD. ABCD is a trapezoid, my bad didn't mention it, it's quite essential. — Witherik, Jun 17 '20 at 07:07

nonuser · Accepted Answer · 2020-06-16T20:44:19.957

2

Let $X$ be on a ray $DA$ beyond $A$

$\angle CDA = \angle BAX = \angle ACB$ (tangent-chord)
$\angle DAC = \angle ABC$ (tangent-chord)

So triangles $\Delta ADC$ and $\Delta BCA$ are similar, so: $${AC\over AB} = {DC\over AC}\implies AC^2 = AB\cdot DC$$

and thus a conclusion.

edited Jun 16 '20 at 20:44

answered Jun 16 '20 at 20:25

nonuser

91,557

Geometry problem I am having trouble to solve

1 Answers1