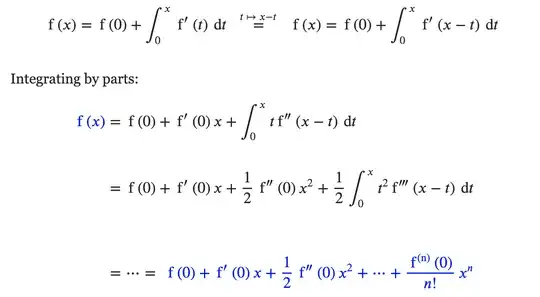As to this beautiful derivation of the Taylor's Theorem, wouldn't it break the equality when we add the term $f(0)$ to the right side of $f(x) = \int_{0}^{x} f'(t)dt$ ?
Asked
Active
Viewed 43 times
0
-
I don't understand your concern. Can you rephrase? Where are you adding $f(0)$ somewhere? – davidlowryduda Jun 11 '20 at 15:30
1 Answers
3
No. The reason is as follows: we have $$ \int_{0}^{x} f'(t) dt = \left [ f(t) \right ] ^ x _ 0 = f(x) - f(0)$$ (not just $f(x)$). Thus: $$f(x)=f(0)+ \int_{0}^{x} f'(t) dt$$
Manuel Norman
- 1,779