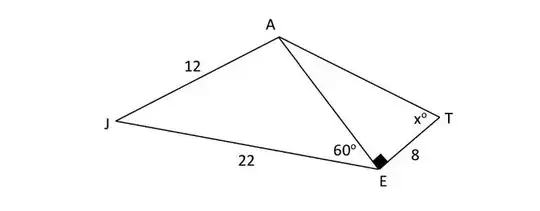
I'm trying to applying the law of sinus in this triangle to get the angle of A. However when I do that I find myself having to do the $sin^{-1} 1.59$ to get A.
This is obtained by having $\dfrac{22}{A} = \dfrac{12}{60}$.
The problem is that it does not work $sin^{-1} 1.59$ gives me a an error 2 message on my calculator. How can I get the angle A if this does not work.
By the law of sines, $$ \frac{22}{\sin A}=\frac{12}{\sin 60^\circ} $$ which yields $$ \sin A = \frac{11\sqrt{3}}{12}\approx 1.59$$ contradiction, since $\sin A$ can't be greater than $1$.
What it means is that there is no such triangle (i.e., it's a trick question).
To further explain, note that the perpendicular distance from the point $J$ to the line $EA$ is $11\sqrt{3}$ which is more than $12$.
The diagram below visually illustrates the issue . . .
Here is a different approach:
Let side $AE$ be $x$. By the law of cosines,
$$\cos 60º = \frac{22^2 + x^2 - 12^2}{2(22)(x)}$$ $$\Rightarrow \frac{1}{2} = \frac{340+x^2}{44x}$$ $$\Rightarrow \frac{22x}{44x} = \frac{340+x^2}{44x}$$ $$\Rightarrow x^2-22x+340=0 \tag{$x \ne 0$}$$
This has discriminant $\Delta = b^2 - 4ac = (-22)^2 - 4(3)(340) < 0$. Therefore, there is no possible value of $AE$ that satisfies the conditions in the triangle.
When two sides are given along with an angle not included between them ( $60^ {\circ}$ is not given between sides $12$ and $22$),
there are three possible situations:
Let the length of normal be $JX=22\sin 60^{\circ}= 19.05$ approximately.
1) The third side length equals $JX$ in the construction of triangle there is tangential contact at $X$, and two points are coincident.
2) If the side side length $12$ is shorter than $JX$, then real solutions do not exist, as happened in this case.
3) When the given length is more than normal length then there would be two solutions to take (like the two small red circles), it cannot be decided which... it is an ambiguous case.
