There are $n$ rectangles packed in a square; all of them are axes-parallel. You are allowed to partition the square into a grid of cells, with $1$ or more rows and $1$ or more columns. You score a point for each cell that contains at least one whole rectangle.
What is the maximum score $s(n)$ you can get, for the worst-case initial arrangement of $n$ rectangles?
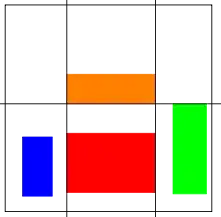
Here are two examples for $n=4$. Here:
your score is 4 (the maximum), since there are 4 cells (out of 6) that contain a whole rectangle. However, here:
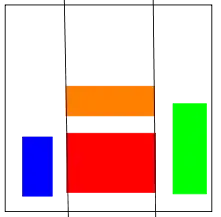
your score is only 3, since there are only 3 cells and each of them contains a whole rectangle (a cell with more than one rectangle is worth only one point). Moreover, here:
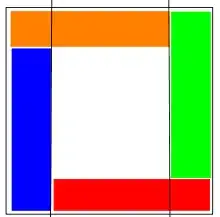
In any grid containing more than 2 cells (e.g. $1\times 3$ or $3\times 1$ or $2\times 2$), at least 2 rectangles are cut, so at most 2 cells contain whole rectangles. This example proves that $s(4)\leq 2$.
On the other hand, it is obvious that you can always score at least $2$ by just taking any two rectangles and creating a $2\times 1$ grid. Therefore $s(4)=s(3)=s(2)=2$.
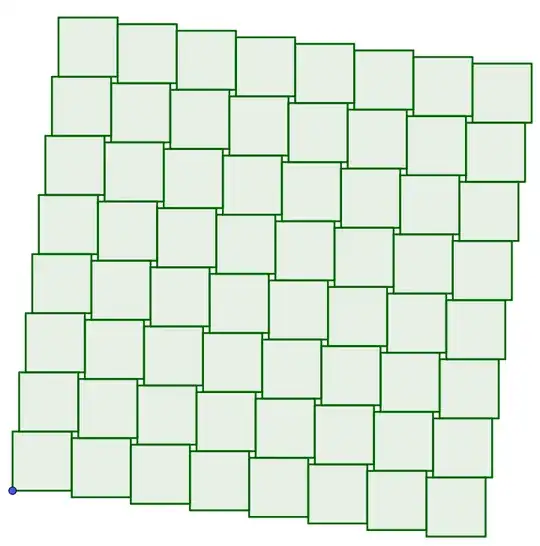
The above example can be generalized by partitioning each rectangle into $n/4$ rectangles, such that each horizontal line cuts at least $n/4$ vertical rectangles and vice-versa. It gives an upper bound of $s(n) \leq \lceil n/2 \rceil$.
Is it always possible to score at least $\lceil n/2 \rceil$? If not, what is the maximum possible score in the worst case?
NOTE: This question is related, but it considers a single cut rather than a grid.