1

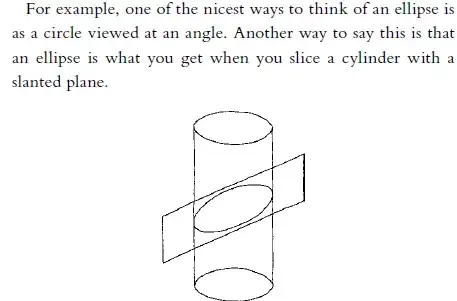
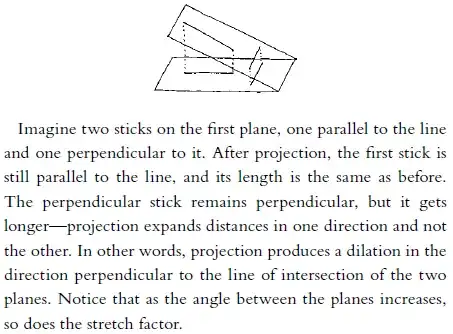
Edit: I've made this question more crisper. The copy-pasted content is from Paul lockhart's Measurement. Below he proves that a parallel projection of a circle onto a tilted plane (Equivalently a cross section of a sliced cylinder) is an Ellipse (defined as a dilated circle). Dilation is like streching a rubber sheet in one direction, rather than zooming in all directions.

enter image description here enter image description here enter image description here

But we know that a suitable cross section of a cone is also an ellipse.

How can we use the same line of above reasoning to prove that it is an ellipse (dilated circle) for central projection (projection lines emerging from a point, in this case the vertex of the cone, rather than from infinity) too ?

enter image description here

  • It's not really clear what you want to ask here. – Berci May 20 '20 at 18:17
  • As for the question, I've highlighted the text in italics. If what you're saying is that the meaning of question is not clear, then please indicate the part where you got lost or make some suggestion as to how I can improve my framing of question. –  May 20 '20 at 19:01
  • 1
    “... central projection (projection lines emerging from a point...) onto a tilted plane is equivalent to a dilation of a plane?” It’s not. With a finite viewpoint, the amount of foreshortening depends on the distance to the viewpoint. With a dilation, the foreshortening is uniform. This question and its answer seem apropos. – amd May 20 '20 at 19:36
  • @Akhil Sorry, I didn't read carefully the full post.. – Berci May 20 '20 at 20:43
  • @Berci I've considerably edited the post to make it less complicated. Please read again. –  May 21 '20 at 05:57
  • See the answer to Why ellipse is a “conic” section?, which appeared previously at MathOverflow. – CiaPan May 21 '20 at 05:59
  • @amd Your comment dispelled one assumption I held: that the center of ellipse must lie on the axis of the cone. –  May 21 '20 at 08:58
  • @CiaPan This answer is the kind of one I'm looking for, but it doesn't finally prove that the curve cut by slanted plane must be a dilated circle (ellipse). –  May 21 '20 at 09:26
  • The answer you link above actually proves nothing. It simply shows it's possible that the section can be an ellipse. In other words, it says it doesn't deny the claim. OTOH the answer I linked shows a proof the curve has a unique property of an ellipse, namely that the sum of distances of any point of a curve from two foci is constant. Which proves the section is an ellipse. – CiaPan May 21 '20 at 11:46
  • @CiaPan I know the dandelin spheres argument, which uses the constant sum property definition of ellipse. What I was looking for is to show it is an ellipse (defined as a dilated circle) without using any other defining properties (constant sum, equal distances, reflection property) of an ellipse. Is that possible? –  May 21 '20 at 14:49
  • You’ve got to have some definition of an ellipse to base that on, though. What is that definition? – amd May 21 '20 at 20:07
  • @amd As I said, the ellipse is defined as a streched circle. –  May 22 '20 at 04:23

0 Answers0