How do you mathematically characterize an "enlarged probability simplex"?

Question

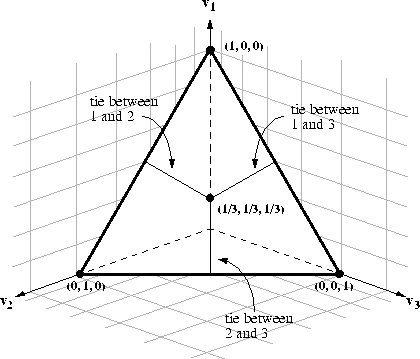
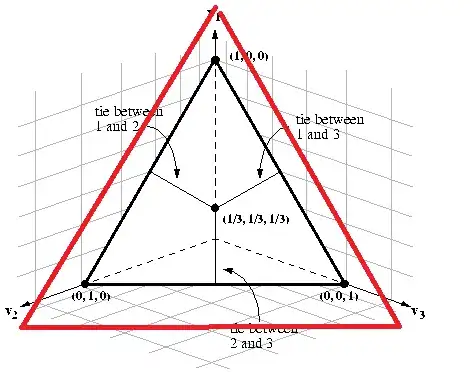
We all know that the probability simplex can be described as the set

$$\Delta = \left\{\theta \in \mathbb{R}^n| \sum\limits_{i = 1}^N \theta_i = 1, \theta_i \geq 0\right\}$$

and in $\mathbb{R}^3$ it is usually drawn as such

I want to characterize a so-called enlarged simplex, the picture looks something like this, where the red lines are the boundary

The restriction is that the enlarged simplex of $\mathbb{R}^n$ must have the same barycenter/center point as the simplex in $\mathbb{R}^n$. In the second diagram, the center point is still $(1/3, 1/3, 1/3)$. In other words, the "enlarged simplex" lies in the same hyperplane which contains the simplex.

How would I go about characterizing such a set? Obviously, $\theta_i \geq 0$ is no longer holds, but removing this constraint gives me a hyperplane, $$\Delta_2 = \left\{\theta \in \mathbb{R}^n| \sum\limits_{i = 1}^N \theta_i = 1\right\}$$ which is not exactly what I want either

$$\Delta_3 = \left\{\theta \in \mathbb{R}^n| \sum\limits_{i = 1}^N \theta_i = \alpha, \alpha > 0, \theta_i \geq 0 \right\}$$ destroys the center point condition.

Answer 1

I guess the enlarged simplex $\Delta'$ is a homothetic image of the basic simplex $\Delta$ with respect to the same center $C=(1/n,\dots, 1/n)$ and the homothety coefficient $\lambda>1$. That is $\Delta'=C+\lambda(\Delta-C)$. Thus the equations of the hyperplanes bounding $\Delta'$ are $$\theta'_i=\frac 1n+\lambda\left(\theta_i-\frac 1n\right)\ge \frac {1-\lambda}n.$$