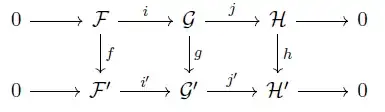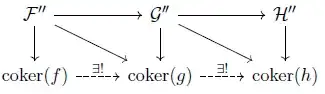I'm trying to prove the snake lemma for sheaves of abelian groups, namely:
If we have the following commutative diagram with exact rows:
Then we have an exact sequence: $$0\to\text{ker}(f)\to\text{ker}(g)\to\text{ker}(h)\to\text{coker}(f)\to\text{coker}(g)\to\text{coker}(h)\to 0$$
The part $0\to\ker(f)\to\ker(g)\to\ker(h)$ is easily constructed from $i,j$ and it's easy to verify it is exact. Now let's call $\mathcal{F}'',\mathcal{G}'',\mathcal{H}''$ the presheaves defined by $U\mapsto \mathcal{F}'(U)/f(\mathcal{F}(U))$, $U\mapsto \mathcal{G}'(U)/g(\mathcal{G}(U))$ and $U\mapsto \mathcal{H}'(U)/h(\mathcal{H}(U))$, whose sheafifications are $\mathcal{F}''\to\text{coker}(f)$, $\mathcal{G}''\to\text{coker}(g)$ and $\mathcal{H}''\to\text{coker}(h)$ respectively. The presheaf morphisms $\mathcal{F}''\to\mathcal{G}''\to\mathcal{H}''$ are naturally induced by $i',j'$ and, using the universal property of sheafification, we get the following commutative diagram:
If I'm not mistaken, we can conclude $\text{coker}(g)\to\text{coker}(h)$ is an epimorphism directly by the fact that $\mathcal{G}'\to\mathcal{H}'$ is an epimorphism.
Now I'm stuck trying to proving that $\text{coker}(f)\to\text{coker}(g)\to\text{coker}(h)$ is exact and I have no idea how to build the connection map $\ker(h)\to\text{coker}(f)$.
Any ideas?