1

can anyone phrase a common definition for the union and intersection for below case.

Actually I am looking for mathematical expression in mathematical notations.

For example if I want to do $G_1 \cup G_2$ or $G_2 \cup G_3$ and $G1 \cap G_2$ or $G_2 \cap G_3$. (*As I feel, the situation is different because one edge and one node is common for (G1, G2) and (G2,G3) respectively)

So, I want to phrase these intersection and union with common variables with mathematical notations (except $G_1, G_2, G_3$).

Here, is my example figure:

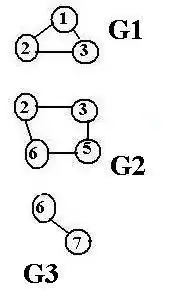
enter image description here

NOTE: I am looking for some mathematical phrasing. for example in Amalgamation of graphs, in the answer, it uses different notation. So, looking for similar phrasing.

Community
  • 1
niro
  • 733

2 Answers2

4

Is this what you were looking for:

$G_1$ is a graph with vertex set $\{1,2,3\}$ and edge set $\{\{1,2\},\{1,3\},\{2,3\}\}$.

$G_2$ is a graph with vertex set $\{2,3,5,6\}$ and edge set $\{\{2,3\},\{3,5\},\{5,6\},\{2,6\}\}$.

So $G_1\cup G_2$ is a graph with vertex set $\{1,2,3,5,6\}$ and edge set $\{\{1,2\},\{1,3\},\{2,3\},\{3,5\},\{5,6\},\{2,6\}\}$. As you can see, I have simply taken the union of the vertex and the edge sets. Similarly $G_1\cap G_2$ is a graph with vertex set $\{2,3\}$ and edge set $\{\{2,3\}\}$. Here I have taken the intersections of the vertex and edge sets. All the others are obtained on similar lines.

  • @: thanks for the answer. but i am looking for something like below phrsing. not a simple list of nodes. http://math.stackexchange.com/questions/251396/amalgamation-of-graphs – niro Apr 20 '13 at 12:58
0

Are you just looking for notation? Say $G$ has vertices $\{a,b,c\}$ and $H$ has vertices $\{1,2,3\}$. Then $$(G\sqcup H)/\{a\sim2\}$$ is the disjoint union of $G$ and $H$ followed by a quotient where we associate the vertex $a$ with the vertex $2$.

In the case of defining $G\cap H$, we would have to define $G$ and $H$ as subgraphs of some common graph first, and then the meaning of the notation $G\cap H$ should be obvious.

Mike Pierce
  • 19,406