Error term in finite differences using Taylor's theorem?

Question

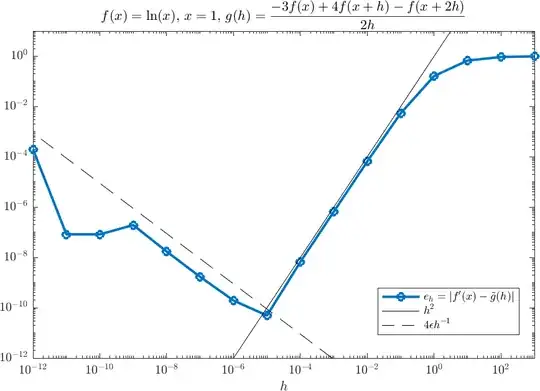
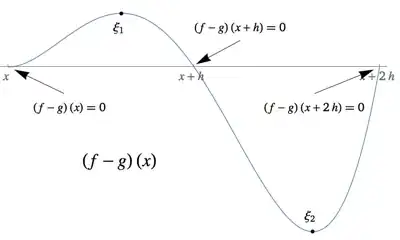
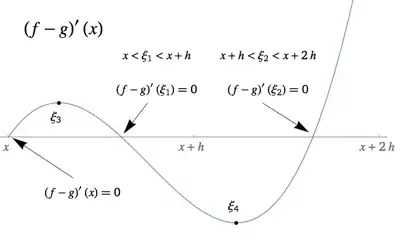
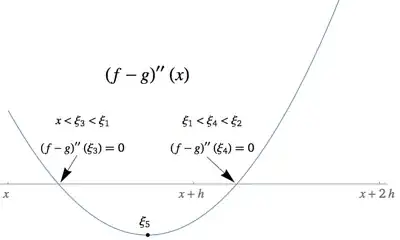
y'all! For my ODEs class in college, we were asked to find the truncation error and round-off error(separately) for this given finite differences problem.

$f'(x) \approx$ $\frac{-3f(x)+4f(x+h)-f(x+2h)}{2h}$

It says we should ignore the round-off errors in h,x,x+h, x+2h?

I am not too sure about the following things:

• Firstly, I thought these were the very terms the errors were coming from. So how can we just ignore these and still be able to compute the error?

• Secondly, I understand that the solution to this problem has to be when we expand this expression using the Taylor series, but I am not too sure how to expand it. The reason I say this is because usually when expanding a function of the form $f(x)$ using the Taylor series, we expand about some point a. But here the function to expand is of the form (x+2h) and (x+h), and I am not even sure which point we are expanding this function about.

• Thirdly, for the round-off error if we are to consider round-off error in each term in the numerator, how do we account for these, just add them up?

• Finally, if someone posts a solution the problem, can you please help me specifically with the Taylor expansions? Our Calculus 2 class did not cover it.

Also, am I able to find a finite difference approximation to the second derivative of f using this?

The way I thought about it was is that in the easiest case of finding second derivative using finite difference, we have that $f''(x) = \frac{f(x+h)+f(x-h)+2f(x)}{h^{2}}$. Should I just replace the values in the above term?

Answer 1

We know from Taylor's theorem that \begin{equation} f(x) = \sum_{k=0}^n \frac{f^{(k)}(a)}{k!}(x-a)^k + O((x-a)^{n+1}), \quad x \rightarrow a, \end{equation} if $f$ is $n+1$ times differentiable in some interval containing $a$. Now let $x$ be fixed (the value at which you want to approximate the derivative of $f$), and we use the formula above with $x$ replaced by $x+h$ and $x+2h$, respectively, and with $a$ replaced by $x$ (so that $x-a = h$ and $x-a = 2h$, respectively). Thus we expand about the fixed $x$: \begin{eqnarray} f(x) &=& f(x),\\ f(x+h) &=& f(x) + f'(x) h + \frac{1}{2} f''(x) h^2 + \frac{1}{6} f^{(3)}(x) h^3 + O(h^4),\\ f(x+2h) &=& f(x) + f'(x) 2h + \frac{1}{2} f''(x) 4h^2 + \frac{1}{6} f^{(3)}(x) 8 h^3 + O(h^4), \end{eqnarray} for $h \rightarrow 0$. Now we form the finite difference \begin{eqnarray} -3f(x) +4f(x+h) -f(x+2h) &=& (-3+4-1)f(x) + (4-2)f'(x)h +\\ && + (4-4)\frac{1}{2} f''(x) h^2 + (4-8)\frac{1}{6}f^{(3)}(x) h^3 + O(h^4)\\ &=& 2 f'(x) h - \frac{2}{3} f^{(3)}(x) h^3 + O(h^4)\\ &=& 2hf'(x) + O(h^3), \quad h \rightarrow 0. \end{eqnarray} Finally, dividing by $2h$, we obtain the difference quotient \begin{equation} \frac{-3f(x)+4f(x+h)-f(x+2h)}{2h} = f'(x) + O(h^2), \quad h \rightarrow 0. \end{equation} Therefore, the given forward difference approximation for the first derivative of $f$ is second-order accurate.

Let us denote the forward difference quotient on the left-hand side by $g(h)$ ($x$ is fixed!). If we evaluate it using finite-precision arithmetic then we will compute a value $\tilde{g}(h) \neq g(h)$. If we consider round-off error only in the evaluation of $f$ at the three points (i. e. we evaluate a function $f_{\epsilon}$ instead of $f$, where $\epsilon$ denotes the machine precision), then we can estimate $|g(h) - \tilde{g}(h)| =$ \begin{eqnarray} && \left|\frac{-3f(x)+4f(x+h)-f(x+2h)}{2h} - \frac{-3f_{\epsilon}(x)+4f_{\epsilon}(x+h)-f_{\epsilon}(x+2h)}{2h}\right|\\ &=& \left| \frac{-3(f(x)-f_{\epsilon}(x)) + 4(f(x+h)-f_{\epsilon}(x+h)) - (f(x+2h)-f_{\epsilon}(x+2h))}{2h} \right|\\ &\leq& \frac{3\epsilon + 4\epsilon + \epsilon}{2h} = \frac{4\epsilon}{h} = O(h^{-1}), \quad h \rightarrow 0. \end{eqnarray} The truncation error and the round-off error are usually split by using the triangle inequality: \begin{equation} e_h := |f'(x) - \tilde{g}(h)| \leq \underbrace{|f'(x) - g(h)|}_{\textrm{truncation error $O(h^2)$}} + \underbrace{|g(h)-\tilde{g}(h)|}_{\textrm{round-off error $O(h^{-1})$}}, \quad h \rightarrow 0, \end{equation} so that they can indeed be treated separately.

As $h \rightarrow 0$ the round-off error will eventually dominate, and this is exactly the behavior you should observe when you plot the approximation error $e_h$ (for specific $f$ and $x$) vs. $h$: in a log-log plot, the error will decrease first with slope $2$, but at some point will increase again with slope $-1$ due to the round-off error. I illustrate this here for $f(x) := \ln(x)$ at $x := 1$ ($f'(x) = 1$):

Answer 2

To the last point, you can write that expression as a combination of easier-to-recognize building blocks, iterated divided differences, $$ \frac{f(x+h)-f(x-h)}{2h}-\frac{h^2}{2}\frac{f(x+2h)-3f(x+h)+3f(x)-f(x-h)}{h^3}. $$ The first term is a second order approximation of the first derivative, and the second term is after the quadratic factor a third order difference quotient, thus at least an $O(h)$ approximation of $f'''(x)$, meaning a bounded expression.

Answer 3

Apply Taylor's Theorem

Taylor's Theorem gives the two equations $$ \begin{align} f(x+h)&=f(x)+hf'(x)+\frac{h^2}2f''(x)+\int_0^hf'''(x+t)\frac{(h-t)^2}2\,\mathrm{d}t\tag{1a}\\ f(x+2h)&=f(x)+2hf'(x)+2h^2f''(x)+\int_0^{2h}f'''(x+t)\frac{(2h-t)^2}2\,\mathrm{d}t\tag{1b} \end{align} $$ Therefore, $$ \begin{align} &\left|\,\frac{-3f(x)+4f(x+h)-f(x+2h)}{2h}-f'(x)\,\right|\tag{2a}\\[3pt] &=\frac1{2h}\left|\,4\int_0^hf'''(x+t)\frac{(h-t)^2}2\,\mathrm{d}t-\int_0^{2h}f'''(x+t)\frac{(2h-t)^2}2\,\mathrm{d}t\,\right|\tag{2b}\\ &\le\frac1{2h}\left(4\sup_{t\in[0,h]}|f'''(x+t)|\,\frac{h^3}6+\sup_{t\in[0,2h]}|f'''(x+t)|\,\frac{4h^3}3\right)\tag{2c}\\[6pt] &\le h^2\sup_{t\in[0,2h]}|f'''(x+t)|\tag{2d} \end{align} $$ Explanation:
$\text{(2b)}$: apply $\text{(1a)}$ and $\text{(1b)}$ to $\text{(2a)}$
$\text{(2c)}$: $\int_0^h\frac{(h-t)^2}2\,\mathrm{d}t=\frac16h^3$ and $\int_0^{2h}(2h-t)\,\mathrm{d}t=\frac43h^3$
$\text{(2d)}$: $\sup\limits_{t\in[0,h]}|f'''(x+t)|\le\sup\limits_{t\in[0,2h]}|f'''(x+t)|$

Thus, $$ \bbox[5px,border:2px solid #C0A000]{\left|\,\frac{-3f(x)+4f(x+h)-f(x+2h)}{2h}-f'(x)\,\right| \le h^2\sup_{t\in[0,2h]}|f'''(x+t)|}\tag3 $$

---

Extension of the Mean Value Theorem

Let $$ \begin{align} g(x+ht) &=\left(f(x)+\left(hf'(x)+\tfrac32f(x)\right)t\right)\frac{(t-1)(t-2)}2\\ &-f(x+h)\,t^2(t-2)+f(x+2h)\,\frac{t^2(t-1)}4 \end{align}\tag4 $$ Then it is easy to verify that $$ \begin{align} g(x)&=f(x)&g'(x)&=f'(x)\\ g(x+h)&=f(x+h)&g(x+2h)&=f(x+2h) \end{align}\tag5 $$ Equations $(5)$ implies $$ (-3I+4S_h-S_{2h}-2hD)(f-g)(x)=0\tag6 $$ where $S_h$ is the shift operator: $S_hf(x)=f(x+h)$; and $D$ is differentiation: $Df(x)=f'(x)$.

Since $$ (-3I+4S_h-S_{2h}-2hD)\left(1,x,x^2,x^3\right)=\left(0,0,0,-4h^3\right)\tag7 $$ and $g(x)$ is a cubic polynomial, we get that $$ (-3I+4S_h-S_{2h}-2hD)g(x)=-\tfrac23g'''(\xi)\,h^3\tag8 $$ for all $\xi$ (since $g'''$ is a constant).

According to $(5)$, $$ \begin{align} (f-g)(x)&=0\\ (f-g)(x+h)&=0\\ (f-g)(x+2h)&=0 \end{align}\tag9 $$

According to $(5)$ and Rolle's Theorem applied to $(9)$: $$ \begin{align} (f-g)'(x)&=0\\ (f-g)'(\xi_1)&=0&x\lt\xi_1\lt x+h\\ (f-g)'(\xi_2)&=0&x+h\lt\xi_1\lt x+2h \end{align}\tag{10} $$

Applying Rolle's Theorem to $(10)$: $$ \begin{align} (f-g)''(\xi_3)&=0&x\lt\xi_3\lt\xi_1\\ (f-g)''(\xi_4)&=0&\xi_1\lt\xi_4\lt\xi_2 \end{align}\tag{11} $$

Applying Rolle's Theorem to $(11)$: $$ \begin{align} (f-g)'''(\xi_5)&=0&\xi_3\lt\xi_5\lt\xi_4 \end{align}\tag{12} $$

Therefore, for some $\xi_5$ between $x$ and $x+2h$, we have $$ \begin{align} -\tfrac23f'''(\xi_5)h^3 &=-\tfrac23g'''(\xi_5)\,h^3\tag{13}\\ &=(-3I+4S_h-S_{2h}-2hD)g(x)\tag{14}\\[3pt] &=(-3I+4S_h-S_{2h}-2hD)f(x)\tag{15} \end{align} $$ Explanation:
$(13)$: apply $(12)$
$(14)$: apply $(8)$
$(15)$: apply $(5)$

Rewriting $(15)$ gives $$ \bbox[5px,border:2px solid #C0A000]{\frac{-3f(x)+4f(x+h)-f(x+2h)}{2h}-f'(x)=-\tfrac13f'''(\xi)\,h^2}\tag{16} $$ for some $\xi\in(x,x+2h)$.