1

Let, $(G,*)$ is a group. We know, no entry appears twice in the Cayley table of this group.

Now let, a Cayley Table is given with no entry appearing twice in a row or column. Let, the existence of identity and inverses are guaranteed in Cayley Table. Then without checking associativity can we say that this Cayley table does represent a group?

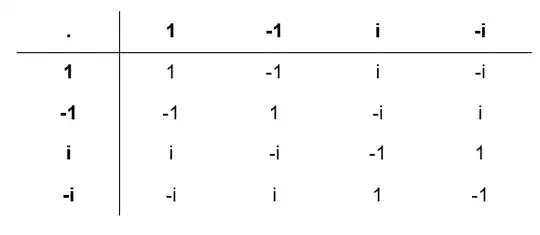
For example, consider the Cayley Table for $C=\{1, -1, i, -i\} $ under binary operator $.$

caylay table for complex group

Here we can easily identify $1$ as a identity. Also we notice that, $1.1=(-1).(-1)=i.(-i)=(-i).i=1$ which guarantees existence of inverse. Now do we need to check associativity to declare $(C, .)$ a group?

Syed Emad Uddin
  • 172

3 Answers3

2

As for your first question, the answer is no. The smallest non-associative Latin square has order $5$, for example the following: $$\begin{array}{c|ccccc} * & 1 & 2 & 3 & 4 & 5 \\\hline 1 & 1 & 2 & 3 & 4 & 5 \\ 2 & 2 & 1 & 4 & 5 & 3 \\ 3 & 3 & 4 & 5 & 1 & 2 \\ 4 & 4 & 5 & 2 & 3 & 1 \\ 5 & 5 & 3 & 1 & 2 & 4 \tag0 \end{array}$$ Alternatively (but not more efficiently) than checking the triplets to assess the associativity, you can check whether for every $i,j,k\in\{1,\dots,5\}$: $$i*j=k\Longrightarrow \sigma_i\sigma_j=\sigma_k\tag1$$ where $\sigma_i\in S_5$ is defined by: $$\sigma_i(j):=i*j\tag2$$ For the Latin square $(0)$, the definition $(2)$ yields: \begin{alignat}{1} &\sigma_1=() \\ &\sigma_2=(12)(345) \\ &\sigma_3=(13524) \\ &\sigma_4=(14325) \\ &\sigma_5=(15423) \\ \end{alignat} Now, for example, $3*5=2$ but $\sigma_3\sigma_5=(125)\ne\sigma_2$. According to the "associativity test" $(1)$, this is sufficient to state that the composition law $*$ is not associative, and hence $(0)$ is not the Cayley table of a group.

Kan't
  • 4,819
0

Associativity is not implied by the Cayley table. For example take $X$ to be a finite set, $\mathcal P(X)$ be its power set. The set difference operation (which is a binary operation) on $\mathcal P(X)$ is not associative : $(A\setminus B)\setminus C\ne A\setminus(B\setminus C)$. If you draw its Cayley table you can see no two elements in a row are the same.

Existence of identity, commutativity, existence of inverses are all implied by the Cayley table.

Jimmy
  • 1,585
  • If $\phi$ is the empty set, then the set difference $\phi-A=\phi$ for all $A$, so all elements in the row for $\phi$ are equal. – Gerry Myerson Sep 27 '24 at 11:32
  • 1
    This is not a counterexample. Gerry Myerson already observed that one of the row will have all its elements equal. Also, there will be no identity element since there is no set $E$ such that $A\setminus E = E \setminus A = A$ for all sets $A$. – jjagmath Sep 27 '24 at 11:59
  • The only case where this could be you a Cayley table with identity element is when $X=\emptyset$, but then $\mathcal P(X)$ does become a group. – jjagmath Sep 27 '24 at 12:02
0

The question is whether a table in which no element appears twice in any row or column is necessarily a group table. This example shows the answer is no:

Consider the binary operation on the set $\{\,a,b,c,d,e\,\}$ given by the following table:

$$\matrix{e&a&b&c&d\cr a&e&c&d&b\cr b&d&e&a&c\cr c&b&d&e&a\cr d&c&a&b&e\cr}$$

$e$ is the unique identity element, and each element appears exactly once in each row and in each column. We don't have to check associativity to see that this can't be a group table: each element satisfies $x^2=e$, so each non-identity element has order two, but a group of order five can't have any elements of order two (the order of an element in a finite group must divide the order of the group).

If desired, we could give an example of the failure of associativity:
$a(bd)=ac=d$, $(ab)d=cd=a$, so $a(bd)\ne(ab)d$.

My thanks to user @Kan't for pointing out a typo in the table, which I have now corrected.

Gerry Myerson
  • 185,413
Gerry Myerson
  • 3,486