I'm studying the following dynamical system, \begin{align} \dot{x} &= y \,\, , \\ \dot{y} &= \frac{\left(-4 x^3+33 x^2-78 x+54\right) y^2+(x-3) (2 x-6)^2}{(3-2 x) (2-x) x (2 x-6)} \,\, , \end{align}
and when I plot the phase space I get the following graph:
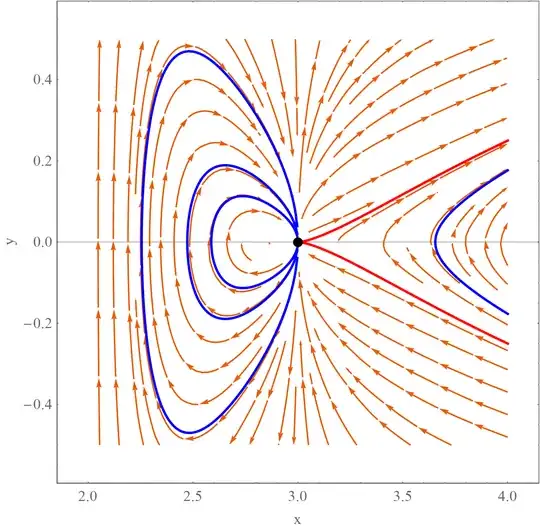
I don't know what is this kind of fixed point, it looks like a half saddle - half center, but there is no fixed point inside the closed orbit, but it is on this orbit. The linear stability isn't conclusive in this case (both eigenvalues are 0).
Ps: The blue and red lines are the curves of the first integral in this system. I used this first integral as Lyapunov function of the system and I checked that exactly in this fixed point, (x,y) = (3,0), there is an inflection point and the test is also inconclusive. Any clues about what is this kind of fixed point and how can I infer its stability?