Obviously I don't need to say that I'm still a newbie, so I'll try to explain my question with some pics too.
I have a infinite set $T$ I have a visual idea of how this set is ordered, but I don't know the name of this kind of order, and what are the statements that define it. (for example total order is defined by antisymmetry, transitivity and totality) this ordar can be visuelized like that:
if we have this for $A,B\in T$

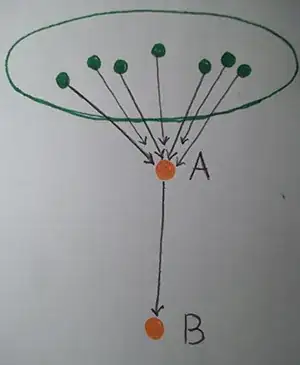
only if $B<A$ and $\nexists C(B<C<A)$ with this we can see the set in this way
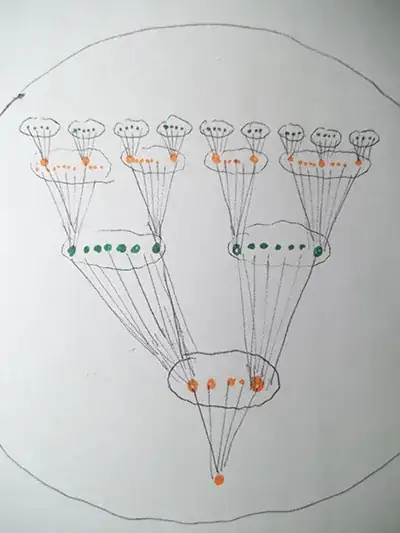
in other words from every element $A\in T$ there are $\kappa$ numbers ($\kappa \ge \aleph_0)$ of elements $G_i$ (the green points) such that $A<G_i$ and $\nexists C(A<C<G_i)$ but exists only one $B$ such that $B<A$ if $\nexists C(B<C<A)$
I addiction the order is transitive, some elements can't be ordered (for example I cant $G_i$ and $G_j$ in the picture), it doesn't have a max and a min.
What is the name of this order? Is a kind of partial order maybe?
I noticed something, there are a infinite number of infinite subset that are totally ordered by $<$
I would like to know more about this order
EXTRA About how the cardinality of $T$ depends from the number of "branches" $\kappa$ ($\kappa$ infinite).
I'm a bit ashamed to show this but this is my naive approach to evaluating $|T|$
$\forall A (A\in T) \exists \beta_A(|\beta_A|=\kappa)$ that set $\beta_A $ is the set I showed in the picture as a green circle and all the sets are disjoint. My naive approach is that $|T|=|\bigcup \beta_{A\in T}|$ that is like the sum $\kappa$ $|T|$ times. In other words my idea is $|T|=|T|\times \kappa$ so if $\kappa$ is countable infinity, the cardinality of $T$ can be every infinite cardinal. Is correct my approach?