6

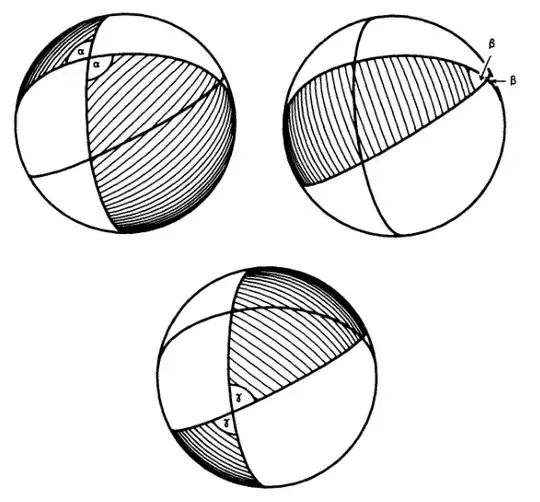
The area of a spherical triangle with angles $\alpha$, $\beta$ and $\gamma$ on the 2-dimensional unit sphere is $\alpha + \beta + \gamma - \pi$. There is a nice geometrical proof of this fact that only uses the fact that the area of the whole sphere is $4\pi$, and the intuitively obvious fact that two great circles that cut at an angle $\alpha$ (necessarily in two antipodal points), bound two slices whose common area is $4\alpha$.

To prove it, you can construct three such (pairs of) regions, that together disjointly cover the sphere except for the triangle and its antipodal image, which are both triply covered, from which it follows. The following image, from Jeffrey Weeks' The Shape of Space, make it very clear:

Area of Spherical Triangles

The corresponding fact for hyperbolic triangles (on the hyperbolic plane with curvature -1) is

$$A = \pi - (\alpha + \beta + \gamma).$$

Would it be possible to prove this is a similar way? Obviously it cannot directly be related to the area of the whole space, but maybe it can be related to the area of some standard triangle, like the one all of whose angles are 0 and which can be realized in the upper half-plane model as the triangle bounded by a half circle centered on the real line and two vertical lines. You would just compute the area of this triangle once and for all.

The kind of answer I would like to see is a proof in which you obtain the area of a general triangle in terms of this reference area in some clever way by applying isometries and the fact that the area of a disjoint union is the sum of the areas, and little more (no integration).

doetoe
  • 4,082
  • A diagrammatic proof is given as an answer to a question seeking proofs-without words on MathOverflow. See also Theorem 5.4.9 and Figure 5.4.10 here (via mphitchman.com). – Blue May 02 '20 at 23:13
  • @Blue Very nice! Still not quite as satisfactory, because you still have to prove it for triangles with one non-zero angle, which in your second link is still done manually. Maybe that is inevitable in the hyperbolic case. – doetoe May 02 '20 at 23:31
  • 1
    You could argue that even in the sphere case there is still something to do "manually", i.e. is it intuitively obvious to you that the area of the sphere is $4\pi$? – Ethan Dlugie May 02 '20 at 23:38
  • @EthanDlugie yes, that is true. That is why I tried to ask for a proof that relates it to the area of a single reference shape (which can be considered to be computed once and for all) – doetoe May 02 '20 at 23:41
  • @doetoe Ah I see. I was trying to remember if you could deduce the general area formula from just the area of the ideal triangle (with all three points on the boundary), but I think you still need perform some kind of integration for triangles with only two ideal points. – Ethan Dlugie May 03 '20 at 00:03

1 Answers1

1

Edit: The question is already asked and the same answer appears here: Area of a triangle $\propto\pi-\alpha-\beta-\gamma$

There is in fact a more general argument. For a convex n-gon in the plane, sphere or hyperbolic plain. consider its defect $\delta$ which is defined as $K(-(n-2)\pi+\sum \alpha_i) $ Where $K$ is the curvature. The defect is in fact a positive measure on the space of convex polygons! Indeed, one has:

1) It is positive (possible to prove),

2) It is invariant under isometries,

3) If a big polygon is divided into two smaller ones, then the sum of their defects equals to the defect of the big polygon.

One can show that there is only one such function up to proportion, and obviously the area function satisfies 1)-3). Therefore the defect is equal to the area up to a constant, which can be calculated by looking at one triangle.

Finally, I remark that a more modern approach to these questions is to use the Gauss-Bonnet theorem.

Espace' etale
  • 1,603
  • Thanks for your reply. As for the linked question, it just asks for a proof. The accepted proof is actually the one that I was taught, and it is not what I am looking for (maybe I didn't manage to clearly describe what I had in mind, I guess it's a bit subjective). I also find Gauss-Bonnet a bit unsatisfactory, not only for these reasons, but also because one of the most straightforward ways to prove it actually depends on the area of a triangle in terms of its curvature and angles. – doetoe May 02 '20 at 23:20
  • You mean you look for a proof in the hyperbolic case that's similar to the proof you exhibited in the spherical case? – Espace' etale May 02 '20 at 23:22
  • Exactly! I wonder if that is possible – doetoe May 02 '20 at 23:24