Confusion on the kernel and image of boundary map in terms of computing simplicial homology.

Question

I am learning simplicial homology, and I have a confusion on the computation.

I understand that the boundary map the boundary map $\partial_{n}:C_{n}(X)\longrightarrow C_{n-1}(X)$ takes the form $$\partial\langle V_{0},\cdots, V_{n}\rangle=\sum_{i=0}^{n}(-1)^{i}\langle V_{0},\cdots,\widehat{V}_{i},\cdots, V_{n}\rangle,$$ where $\widehat{V}_{i}$ means you kick out $V_{i}$ coordinate and keep other coordinates and $\langle V_{0},\cdots, V_{n}\rangle$ is the vertices of $n-$dimensional simplex $\Delta^{n}$.

I also know how to prove that $\partial_{n}\circ \partial_{n+1}=0$ so that you have a chain complex. Then the simplicial homology is defined by $$H_{k}(X)=\ker(\partial_{k})/Im(\partial_{k+1}).$$ However, I don't know how to compute the $\ker$ and $Im$.

For instance, let us take the $2-$dimensional torus $\mathbb{T}^{2}$ as an example:

Consider the well-known triangulation of $\mathbb{T}^{2}$, see here: Computing the first simplical homology group of the torus $H_1(T)$

We have $9$ copies of $\Delta^{0}$, $8$ copies of $\Delta^{1}$ and $18$ copies of $\Delta^{2}$.

Thus, $C_{2}(X)=\mathbb{Z}^{18}$, $C_{1}(X)=\mathbb{Z}^{8}$ and $C_{0}(X)=\mathbb{Z}^{9}$.

Hence, we have chain complex $$C_{2}(X)=\mathbb{Z}^{18}\longrightarrow_{\partial_{2}} C_{1}(X)=\mathbb{Z}^{8}\longrightarrow_{\partial_{1}}C_{0}(X)=\mathbb{Z}^{9}.$$

Now, we compute the $\partial_{2}$ and $\partial_{1}$, we have $$\partial_{2}\langle V_{0},V_{1},V_{2}\rangle=\langle V_{1},V_{2}\rangle -\langle V_{0}, V_{2}\rangle+\langle V_{1}, V_{2}\rangle$$ and $$\partial_{1}\langle V_{0}, V_{1}\rangle=\langle V_{1}\rangle-\langle V_{0}\rangle.$$

But then, what is the image and kernel of $\partial_{1}$ and $\partial_{2}$?

Thank you!

Edit 1: (Update)

As comments pointed out, the group is so large since the simplex is complicated, and thus we need to use sage to compute it. However, the point is that I don't understand how to write down the matrix representation of $\partial_{1}$ and $\partial_{2}$.

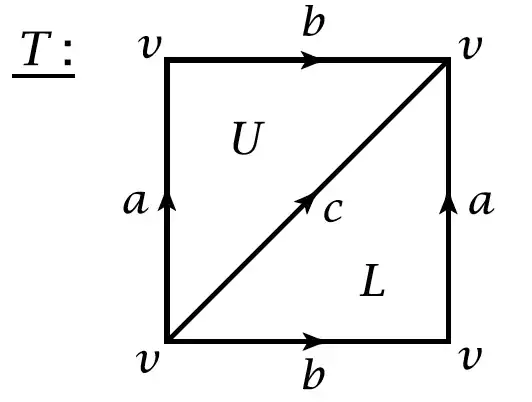
Let me reduce this simplex to this:

The simplex is from Hatcher's book. Then he argued that:

There is one vertex, three edges $a,b,c$ and two $2-$simplices U and L. Then $\partial_{1}=0$ and $\partial_{2}U=a+b-c=\partial_{2}L$, and $\{a,b, a+b-c\}$ is a basis for $\Delta_{1}(T)$, it follows that $H_{1}(T)=\mathbb{Z}\oplus\mathbb{Z}$. Since there are no $3-$simplices, $H_{2}(T)=\ker\partial_{2}$, which is infinite cyclic generated by $U-L$.

I don't understand how he got $\partial_{1}=0$. Given my computation above, $\partial_{1}\langle V_{0},V_{1}\rangle=\langle V_{1}\rangle-\langle V_{0}\rangle$ why $0$?

I also don't understand how he saw that $\{a,b,a+b-c\}$ is the basis for $\Delta_{1}(T)$.

Finally, how to compute $\ker\partial_{2}$?

Answer 1

In your simplified example, $\partial_1$ is zero (since each edge starts and ends at the same vertex, so its boundary is $v-v=0$). So its kernel is the whole chain group $C_1$ and its image is 0. The matrix for $\partial_2$: choose $(U, L)$ for a basis of $C_2$, $(a, b, c)$ for a basis of $C_1$. Then choose an orientation for $U$ and expand $\partial_2(U)$ in terms of $(a, b, c)$ to get an integer vector of coefficients, which goes in the 1st column of the matrix. SageMath will do this for you, too:

sage: T = delta_complexes.Torus()
sage: C = T.chain_complex()
sage: C.differential(1)
[0 0 0]
sage: C.differential(2)
[ 1  1]
[ 1  1]
[-1 -1]

Re computing a basis for $\Delta_1(T)$: I hope it's clear that $(a, b, c)$ is a basis. You can obtain $a+b-c$ from these by invertible linear integer operations, so $(a, b, a+b-c)$ is also a basis. He chose this because $a+b-c$ is the boundary of both $U$ and $L$, so the subgroup spanned by it is the image of $\partial_2$.

Answer 2

The symbols $V_0,V_1$ should be treated as variables, they do not form the vertex set of $T$.

Instead, in your pictorial example, the vertex set of $T$ is $\{v\}$. Also, the edge set is $\{a,b,c\}$.

So, you need to compute $\partial_1 a$, $\partial_1 b$, $\partial_1 c$. You can use the formula $$\partial_1 \langle V_0,V_1 \rangle = V_1 - V_0 $$ as a guide for this computation if you treat $V_0,V_1$ as vertex variables which are to be substituted by actual vertices of $T$: whichever edge is under consideration at the moment, one substitutes $V_0$ for the initial vertex of that edge, and $V_1$ for the terminal vertex of that edge.

For example, to compute $\partial_1 a$, for $V_0$ you substitute the initial vertex of $a$ which is $v$, and for $V_1$ you substitute the terminal vertex of $a$ which is also $v$, and you get $$\partial a = V_1 - V_0 = v - v = 0 $$ Similar considerations apply to give $\partial_1 b = 0$ and $\partial_1 c = 0$.