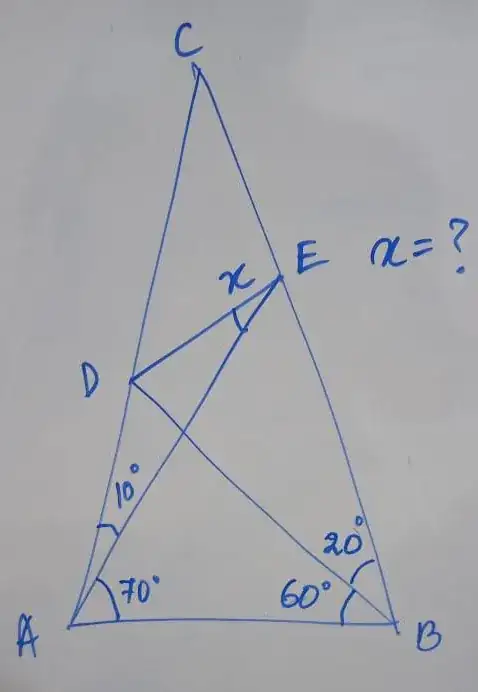
I have found $\angle BDE+x=130^\circ$. But I can solve from this. How can I find $x$?
Asked
Active
Viewed 1,155 times
0
-
Inspect each triangle and write down all the angle measures. – Andrew Chin Apr 29 '20 at 06:56
-
@AndrewChin, maybe I'm wrong, but I don't want to confuse the OP. $\measuredangle=40^{\circ}$ and $\measuredangle BCA=20^{\circ}$, but this isn't a right-angle triangle... and $\Delta ABD$ isn't isosceles.... so it is useless, isn't it? – Matcha Latte Apr 29 '20 at 08:02
-
See https://math.stackexchange.com/questions/3620825/langleys-adventitious-angles/3621250#3621250 – Quanto Apr 29 '20 at 12:57
1 Answers
1
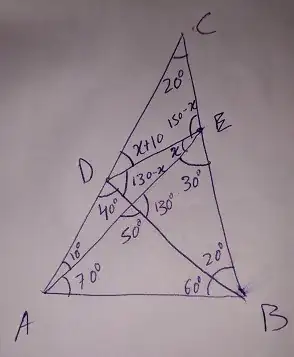
Try expressing all angles in terms of $x$. You should get the following:
Now use Law of sines to get the following relations:
From Triangle $ABE$,
$$\
\frac{BE}{\sin(70)} = \frac{AB}{\sin(30)} \quad \text{ and } \quad \frac{BE}{\sin(70)} = \frac{AE}{\sin(80)}
$$
From Triangle $ADB$,
$$\
\frac{AD}{\sin(60)} = \frac{AB}{\sin(40)}
$$
From Triangle $ADE$,
$$\
\frac{AD}{\sin(x)} = \frac{AE}{\sin(170-x)}
$$
Solving the above equations we get,
$$\
\frac{\sin(60)}{\sin(40)\sin(x)} = \frac{\sin(80)}{\sin(30)\sin(170-x)}
$$
Finally,
$$\
\implies x=20 \deg
$$
Note: All angles are in degree.
Link: Wolframalpha Solution to Trignomteric Equation
Shiv Tavker
- 1,652