It is well known that Euler-Mascheroni constant has an alternative definition in terms of zeta function:
$$ \gamma=\lim_{s\to1^+}f(s)\equiv\lim_{s\to1^+}\left[\zeta(s)-{1\over s-1}\right] $$
Using this definition, I would like to derive the Laurent series expansion for Riemann zeta function, but I am currently stuck because I am in a hard time trying to show the convergence of the following limit:
$$ \lim_{s\to1^+}{\mathrm{d}^n\over\mathrm{d}s^n}f(s) $$
My attempt was to show that the function $f(s)$ is analytic in $\mathbb{C}\setminus\{1\}$ and continuous in $\mathbb{C}$ (by setting $f(1)=\gamma$), and prove that it is entire using Morera's theorem. Using analytic continuation, I am able to express zeta functon in terms of a contour integral:
$$ \zeta(s)=\Gamma(1-s)g(s)\equiv{\Gamma(1-s)\over2\pi i}\oint_C{z^{s-1}\over e^{-z}-1}\mathrm{d}z $$
where the contour $C$ is shown below:
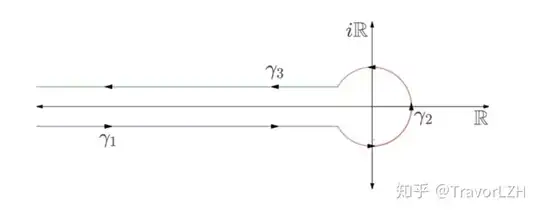
Therefore, $f(s)=\Gamma(1-s)g(s)-{1\over s-1}$, which is already analytic every where except for $z=1$, so how can I show that it is continuous at $z=1$ so that I can prove $f(s)$ to be entire using Morera's theorem?