Characteristics and blow up time of a PDE

Question

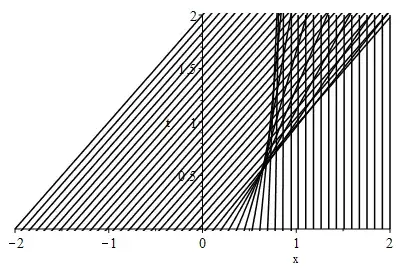
I am trying to picture the characteristic projections of

$$\dfrac{\partial u}{\partial t}+u^2\dfrac{\partial u}{\partial x}=0 \text{ with }x\in\mathbb{R} \text{ and } t>0$$ with the initial data $$u(x,0)=\begin{cases} 1 & x<0 \\ (x-1)^2(2x+1) & 0\leq x\leq 1 \\ 0 & x>1 \end{cases}$$

Then I want the blow up time. Do I need to solve the equation to find the blow up time? For the characteristic projections, parametrise $x\equiv x(t)$

$$\frac{du}{dt}=0, \frac{dx}{dt}=u^2(x,t)$$

The solution is constant along characteristic projectons, with respect to $t$, so I can trace back to the initial curve (usually called $\Gamma$?) setting $x(0)=0$ (am I allowed to do this?)

$$x=(u(x,0))^2=\begin{cases} t & x<0 \\ (x-1)^4(2x+1)^2t & 0\leq x\leq 1 \\ 0 & x>1 \end{cases}$$

When I integrated $\frac{dx}{dt}$ I assumed $u^2(x,t)=u_0(x)$, is this the correct thing to do also? The characteristic projections are quite obvious for either side of the interval $[0,1]$ they are simply the family of curves with $\frac{dx}{dt}=1$ on the left and $\frac{dx}{dt}=0$ (vertical) on the right. I am unsure how to draw the projections elsewhere.

Next the condition for the blow-up is $t=-\frac{1}{F'(x)}$ where $x=F(x)t$ are the characteristic projections. I think that it is when the second derivative of these projections is such that the curves are concave because then they intersect at some point and behave badly. $F''(x)>0$ for $x\in(0,\frac{1}{2}]$ so to find the first blow-up time I need to find the smallest value for $$t=-\frac{1}{F'(x)}=-\frac{1}{12 (x-1)^3 x (1+2 x)}$$ Differentiate; $\frac{dt}{dx}=\frac{10 x^2-1}{12 (x-1)^4 x^2 (2x+1)^2}$ the extreme value is found to be $x=\frac{1}{\sqrt{10}}\in(0,\frac{1}{2}]$ this gives a value $$t=\frac{25 \left(25+34 \sqrt{10}\right)}{6561}$$

I am then asked to show that the solution blows up for a value which turns out to to be around $t=0.527$, slightly higher than $t=0.505$ (above), so can I say that the solution blows up for a time earlier than this, hence it blows up for $t=0.527$ also? Is there a better way to show that a solution blows up for a given time, $t$?

Answer 1

You calculated the solution wrongly. Here is the correct procedure for calculating the solution:

Follow the method in http://en.wikipedia.org/wiki/Method_of_characteristics#Example:

$\dfrac{dt}{ds}=1$ , letting $t(0)=0$ , we have $t=s$

$\dfrac{du}{ds}=0$ , letting $u(0)=u_0$ , we have $u=u_0$

$\dfrac{dx}{ds}=u^2=u_0^2$ , letting $x(0)=f(u_0)$ , we have $x=u_0^2s+f(u_0)=u^2t+f(u)$ , i.e. $u=F(x-u^2t)$

$u(x,0)=\begin{cases}1&x<0\\(x-1)^2(2x+1)&0\leq x\leq1\\0&x>1\end{cases}$ :

$\therefore u=\begin{cases}1&x-u^2t<0\\(x-u^2t-1)^2(2x-2u^2t+1)&0\leq x-u^2t\leq1\\0&x-u^2t>1\end{cases}$

Hence $u(x,t)=\begin{cases}1&x<t\\(x-1)^2(2x+1)&0\leq x\leq1~\text{and}~t=0\\\text{roots of}~(x-u^2t-1)^2(2x-2u^2t+1)-u=0&0\leq x-(\text{square of roots of}~(x-u^2t-1)^2(2x-2u^2t+1)-u=0)\times t\leq1~\text{and}~t\neq0\\0&x>1\end{cases}$

For calculating the blow up time, you should consider the implicit function $u=(x-u^2t-1)^2(2x-2u^2t+1)$ .

Some background information about the implicit function $u=(x-u^2t-1)^2(2x-2u^2t+1)$ : http://www.wolframalpha.com/input/?i=u%3D%28x-u%5E2t-1%29%5E2%282x-2u%5E2t%2B1%29

Answer 2

Here is a plot of the base characteristics, which seem to intersect at $t\approx 0.5$:

As specified in this post, computing the solution isn't necessary to evaluate the breaking time \begin{aligned} t_b = \frac{-1}{\underset{0< x< 1}{\inf} \partial_x u^2(x,0)} &= \frac{-1/12}{\underset{0< x< 1}{\inf} (x - 1)^3 x (2 x + 1)} \\[5pt] &= \frac{125/3}{34\sqrt{10} - 25} \, , \end{aligned} which may be approximated by $t_b \approx 0.5049$. The result in OP is correct.