1

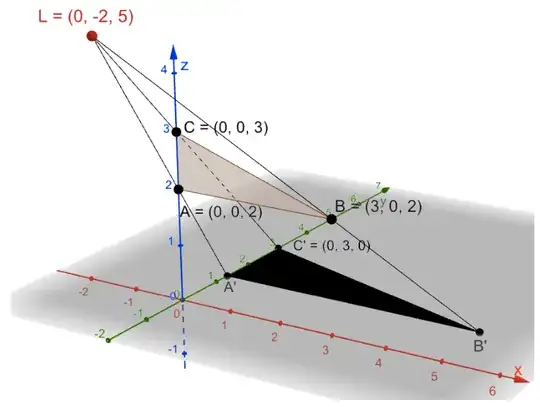
Problem

We have a light source in $L = (0, -2, 5)$, and we have a triangle $ABC$, given by the points $(0, 0, 2), \ (3, 0, 2), \ (0, 0, 3)$.

We are also given that the point $C$ projects to $C' = (0, 3, 0)$ on the $xy$ plane.

Find the area of the shadow created by the triangle on the $xy$ plane.

enter image description here

Thoughts

I don't see the importance of giving us the $C'$ point, seeing as we still need to find $A'$, $B'$ ourselves anyway, right?

The best method I can think of is finding these two points, and then we can simply calculate the area of the shadow using, for example, the cross products of two vectors that span it.

But the problem seems to be hinting at some generalized way of calculating the area of the projection of the triangle onto a plane.

Community
  • 1
Alec
  • 4,174
  • To be clear: For the generalization, are you still interested specifically in projecting an arbitrary triangle in space onto an arbitrary plane? "Projecting a surface onto another surface" would seem to suggest an interest in potentially non-triangular and non-planar regions, which would be complicated to tackle in general. – Blue Apr 22 '20 at 09:04
  • @Blue - For the context of this problem, I'm only really interested in this particular triangle. But my curiosity extends to any arbitrary triangle. If an answer were to outline that, that'd be ideal. For the record, I am NOT caught up in projecting arbitrary 3D objects onto a 2D plane just yet. Baby steps etc. – Alec Apr 22 '20 at 09:07
  • Just checking. :) I've taken the liberty of focusing the problem statement. – Blue Apr 22 '20 at 09:13

2 Answers2

1

If, sooner or later, you are asked the area of the projected are, here is a way to do it.

Let us consider, for the sake of simplicity, that the center of central projection $L$ has coordinates $(0,0,h)$ (i.e., is situated on $z$ axis). If it is not the case, translate your figure in such a way that this is so.

It is not difficult to see that the image of point $(x,y,z)$ is point $(X,Y,0)$ with

$$X=\dfrac{hx}{h-z}=p(x,y), \ \ Y=\dfrac{hy}{h-z}=q(y,z)$$

Then, the area of the projected triangle is (see for example here) :

$$\dfrac12 \begin{vmatrix}p(x_1,y_1)&p(x_2,y_2)&p(x_3,y_3)\\q(y_1,z_1)&q(y_2,z_2)&q(y_3,z_3)\\1&1&1\end{vmatrix}$$

which can be written :

$$\dfrac{h^3}{2(h-z_1)(h-z_1)(h-z_1)} \begin{vmatrix}x_1&x_2&x_3\\y_1&y_2&y_3\\1-\tfrac{z_1}h&1-\tfrac{z_2}h&1-\tfrac{z_3}h\end{vmatrix}$$

Verification : if $h\to +\infty$, we tend to the situation of vertical projection, and we find back the area of triangle

Jean Marie
  • 88,997
-1

Hint. Find the points $A'$ and $B'.$ We have that the line $LA$ lies in the $yz$ plane, so that its equation is given by $2z=4-3y,$ and on setting $z=0$ we find that $y=4/3.$

Now since the triangle $ABC$ lies in the $xz$ plane, and has orthogonal dimensions $AC=1$ and $AB=3,$ we see that $A'C'=5/3,$ so that the scale factor is $5/3.$ Hence the area of $A'B'C'$ is given by $$\left(\frac53\right)^2\left(\frac12×3×1\right).$$

Allawonder
  • 13,583
  • Let me see if I got this right: The scale factor would be $S = \frac{\left|\vec{LC'}\right|}{\left|\vec C\right|}$ and then the area of the shadow would be $S^2\cdot(\text{area of original triangle})$? – Alec Apr 22 '20 at 14:46