2

I'm trying to work out the proof of lemma 55.3 in Munkres' Topology, and I'm missing a detail at the beginning.

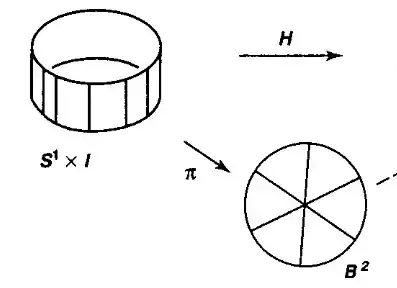
Let $B^2$ denote the unit disk, $S^1$ the unit circle, and $I = [0,1]$. The proof begins by defining a map $\pi : S^1 \times I \to B^2$ such that $\pi(x,t) = (1-t)x$. The following figure gives a good intuition on the definition of $\pi$.

The proof of the lemma relies on the fact that $\pi$ is a quotient map. This is where I'm missing something. Munkres states without further details that $\pi$ is a continuous, closed and surjective map. I see that $\pi$ is indeed surjective, and I know from basic analysis that it is continuous. However, it doesn't seem so obvious to me that $\pi$ is closed. Why is it the case? I think I get the intuition from the figure, but I'm not sure how to prove it.

Vincent
  • 736

1 Answers1

2

A continuous function from a compact space to a Hausdorff space is closed.

$B^2$ is clearly Hausdorff as a subset of a metric space. $S^1 \times I$ can be thought of as a closed and bounded subset of $\mathbb{R}^3$ hence is compact.

Physical Mathematics
  • 4,673
  • Wow thanks, I hadn't thought of that, it's a pretty good way to see it. – Vincent Apr 19 '20 at 19:46
  • I think it's the best/most straightforward way. I always find it a little odd to use a trick like this to see this when it feels like there should be a more direct proof. I think any direct proof would require more working than proving all the relevant details of the above proposition though. Also please accept the answer if your question is resolved – Physical Mathematics Apr 19 '20 at 19:49
  • 1
    Yes it is indeed very straightforward! I'll try to remember that. And I should accept your answer soon, I just thought 15 minutes was a little short delay and that I should wait in case somebody else had another brilliant idea. – Vincent Apr 19 '20 at 19:56