0

Im wondering about the difference of an I-state-space controller and an (simple) PI-Controller?

As I know, you get the advantage to place any dynamic with the state-space-control (if the manipulating variable is without limit).. but what else can be pointed to use an I-state-space controller?

I-State-Space-Controller

PI Control

rst_tk
  • 115
  • For first order systems there is no real difference. But for higher orders, the state-space controller uses more feedback signals (and therefore more information) than PI. – SampleTime Apr 14 '20 at 16:18
  • Yes I know. Using more information is useful and might enhance the performance.. but how? – rst_tk Apr 14 '20 at 16:19
  • What do you mean by "how"? How to use a state-space controller (i.e. design the $K$ matrix)? – SampleTime Apr 14 '20 at 16:23
  • No, I have calculated a state space I controller for control of an second degree system. But afterwards I’m asking what the real difference is to an PI-Controller. I used pole placement with an coefficient comparison of the closed-loop tfunc to get the parameters k1,k2,Ki.. that way is also valid for calculating the PI-Control params.. so im asking what is the real advantage – rst_tk Apr 14 '20 at 16:25
  • I added an answer... just one more note: $e = w - y$, not $\dot{e} = w - y$, like in your image. – SampleTime Apr 14 '20 at 19:17

1 Answers1

4

Take the second order system

$$ G(s) = \frac{1}{s^2} \tag{1} $$

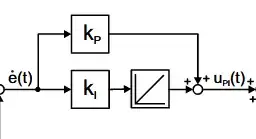
and a PI controller

$$ C(s) = k_p + \frac{k_i}{s} $$

The closed loop transfer function is

$$ G_{cl}(s) = \frac{k_p s + k_i}{s^3 + k_ps + k_i} $$

Can this system be stable? We know that a necessary condition is that the coefficients of the denominator polynomial of $G_{cl}(s)$ are positive. However, the $s^2$ coefficient is zero.

Conclusion: The second order system $(1)$ cannot be stabilized with PI control.

Now lets look at a state feedback controller with integral action. The transfer function $(1)$ in state space is

$$ \begin{align} \dot{x} &= A x + Bu \\ y &= C x \end{align} $$

with

$$ A = \begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix}, B = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, C = \begin{bmatrix} 0 & 1 \end{bmatrix}, x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $$

The integral controller is

$$ \begin{align} \dot{x}_i &= e = w - y \\ u_i &= k_i x_i \end{align} $$

You can put that together:

$$ \begin{align} \dot{\xi} &= \begin{bmatrix} A & 0 \\ -C & 0 \end{bmatrix} \xi + \begin{bmatrix} B \\ 0 \end{bmatrix} u + \begin{bmatrix} 0 \\ 1 \end{bmatrix} w \\ y &= \begin{bmatrix} C & 0 \end{bmatrix} \xi \\ \xi &= \begin{bmatrix} x_1 \\ x_2 \\ x_i \end{bmatrix} \end{align} $$

and design a control law with $u_x = \begin{bmatrix} k_1 & k_2\end{bmatrix} x$ and $u_i = k_i x_i$ so

$$ u = -u_x - u_i = -K_a \xi = -\begin{bmatrix} k_1 & k_2 & k_i \end{bmatrix}\xi $$

This will give you a closed loop transfer function:

$$ G_{cl} = \frac{-k_i}{s^3 + k_1 s^2 + k_2 s - k_i} $$

This will be stable as long as you take $k_1, k_2 > 0$, $k_i < 0$ and $k_1 k_2 + k_i > 0$.

Conclusion: The second order system $(1)$ can be stabilized with state feedback + integral action.

Example: Take $k_1 = 6$, $k_2 = 11$, $k_i = -6$ for the closed loop transfer function

$$ G_{cl} = \frac{6}{(s + 1)(s + 2)(s + 3)} $$

and to place the closed loop eigenvalues at $-1, -2, -3$. This would be impossible using PI control.

With full state feedback, not only can we stabilize the system, we can also put its eigenvalues wherever we want.

SampleTime
  • 3,651