0

I am pretty sure the following topic has already been introduced and studied somewhere, but I have not found references so far, so any help would be gladly welcome!

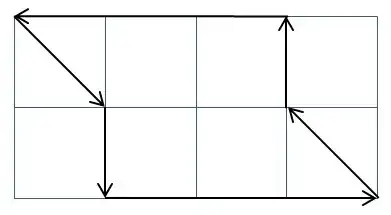
One can define a map $f$ on polygons as follows: assume the boundary of a polygon is seen as a finite set of vectors turning around its interior wrt the trigonometric sense, and consider for any angle $\theta \in [0,\pi[$ the scalar sum of vectors that have the same direction whose argument is $\theta$ mod $\pi$, so that $f$(P) is a map whose parameter is $\theta \in [0,\pi[$ with values in $\mathbb{R}$.

For instance, if T is the triangle whose vertices are $(0;0)$, $(0;1)$ and $(1;0)$ then

$f$(T)($0$)$=1$, $f$(T)($\frac{\pi}{2}$)$=-1$, $f$(T)($\frac{3\pi}{4}$)=$\sqrt{2}$ and f(T)($\theta$)=0 for any other value of $\theta$.

Trivially, for any parallelogram P, $f$(P) is the null function. Is it true that for any polygon P such that $f$(P) is the null function, P is a finite disjoint set of parallelograms? I think the result is yes, but I am not yet able to prove it.

My first thought was to try an induction on $\frac{n}{2}$ where $n$ is the number of sides of P, but I have realized then that it is not so clear that f(P) cannot be the null function when the number of sides of P is odd... thanks in advance for your comments.

Mathieu Dity
  • 341
  • 2
    If you're talking specifically about regular polygons and rhombus parallelograms, take a look at this previous question. – Blue Apr 13 '20 at 12:46
  • 1
    This is a very nice link, thanks! This is closely related to the question I ask here, although I am not totally sure this is exactly the same. I will need some time to read and investigate. – Mathieu Dity Apr 13 '20 at 12:59

2 Answers2

2

The coordinates of the vertices of the polygon below are $(0,0),(2,0),(2,1),(1.2,1),(2.2,2),(1,2),(1,1)$.

Proof that this polygon cannot be decomposed into parallelograms: Suppose that this polygon could be decomposed into parallelograms. Denote the parallelograms in the decomposition which have part of the bottom edge as one of their sides by $S_1,...,S_n$. Let $h$ be the height of the shortest of the $S_i$. Now consider a horizontal line $L$ which is at a height of at most $h$ above the bottom edge. The length of the intersection of $L$ with $S_i$ is the length of the base of $S_i$. Therefore the length of the intersection of $L$ with the polygon is at least the length of the bottom edge, which is clearly false. enter image description here

Angela Pretorius
  • 10,280
1

This is not an answer, just the proposal of a slightly simpler figure associated with the proof of Angela Richardson :

enter image description here

Besides, one can extend this proof of non-existence of a paving by parallelograms to more general polygons by simply taking a trapezoid like this one :

enter image description here

Jean Marie
  • 88,997