I was digging through some old questions I had from high school and I came across this circle geometry problem.
.
There were no solutions unfortunately.
How can this be proven?
Here are a few things I've tried:
Pascal's theorem
Proof that $\angle EBF = \angle EAF$
ABDC is a cyclic quadrilateral
I have been unsuccessful with all of these attempts, however I may have missed something when attempting to prove these.
The required claim follows from Problem 30.38.b from the last section of the first volume (“Plane Geometry”) of the book “Problems in plane and solid geometry” by Viktor Prasolov.
30.38. a) Through point $P$ all secants of circle $S$ are drawn. Find the locus of the intersection points of the tangents to $S$ drawn through the two intersection points of $S$ with every secant.
b) Through point $P$ the secants $AB$ and $CD$ of circle $S$ are drawn, where $A$, $B$, $C$, $D$ are the intersection points of the secants with the circle. Find the locus of the intersection points of $AC$ and $BD$.
The proposed solution:
30.38. Let us consider, separately, the following two cases.
1) Point $P$ lies outside $S$. Let us make the projective transformation that sends circle $S$ into circle $S_1$ and point $P$ into $\infty$ (see Problem 30.17), i.e., the images of all lines passing through $P$ are parallel to each other. Then in heading b) the image of the locus to be found is line $\ell$, their common perpendicular passing through the center of $S_1$, and in heading a) the line $\ell$ with the diameter of $S_1$ deleted.
To prove this, we have to make use of the symmetry through line $\ell$. Therefore, the locus itself is: in heading b), the line passing through the tangent points of $S$ with the lines drawn through point $P$ and in heading a), the part of this line lying outside $S$.
2) Point $P$ lies inside $S$. Let us make a projective transformation that sends circle $S$ into circle $S_1$ and point $P$ into its center, cf. Problem 30.16 a). Then the image of the locus to be found in both headings is the infinite line. Therefore, the locus itself is a line.
The obtained line coincides for both headings with the polar line of point $P$ relative to $S$, cf. Problem 30.19.
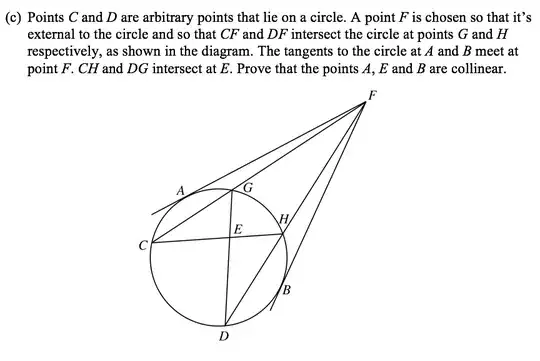
Let $O$ be a circumcenter of the circle, let $M$ be a midpoint of segment (chord) $AB$ and let circles (blue) around $CHF$ and $DGF$ meet at $N$. Also let line $EF$ meet circle at $X$ and $Y$.
Let us prove that
This will mean that $\angle OME = 90^{\circ}$ and thus $E$ lies on $AB$.
Lemma $0$. Points $E,F$ and $N$ are collinear.
Proof: Point $E$ is on a radical axsis for circles $(FGD)$ and $(CHF)$: $$Pow(E,(FGD)) = EG\cdot ED = EC\cdot EH = Pow(E,(CHF))$$ which is $NF$.
Lemma $1$. Points $D,H,N,E$ are concyclic (red circle).
Proof: $$\angle EHN \equiv \angle CHN = \angle CFN = \angle GDN\equiv \angle EDN$$
Lemma $2$. We have $FX\cdot FY = FE\cdot FN$
Proof: $$FX\cdot FY = FH\cdot FD = FE\cdot FN$$
Lemma $3$. We have $EN\cdot EF = EX\cdot EY$
Proof: $$EN \cdot EF = EC\cdot EH = EX\cdot EY$$
Now let us prove that $N$ halves $XY$. Let $FX = s$, $EX= x$, $NE = z$ and $NY = y$.
From lemma 2 we have $$z(x+s)= x(y+z)$$ From lemma 3 we have $$ s(s+x+y+z) = (s+x)(s+x+z)$$
Combining these two (eliminate $s$) we get $y=x+z$ which means that $N$ halves $XY$ and we are done.
Lemma $4$. $ONEM$ is cyclic (yellow).
Proof: $OB\bot BF$ we see that $BF$ is tangent to circle (OMB), so $$FM\cdot FO = FB^2 = FH\cdot FD = FE\cdot FN$$
Changing notation a bit ...
Given $\bigcirc O$ and a point $P$ with tangent segments $\overline{PA}$ and $\overline{PB}$, introduce $\bigcirc P$ through $A$ and $B$. For $C$ and $D$ on $\bigcirc P$, let the extensions of $\overline{PC}$ and $\overline{PD}$ meet $\bigcirc O$ at points $C'$, $C''$, $D'$, $D''$, as shown:
Calculating the power of $P$ with respect to $\bigcirc O$ in three ways, we have $$ pow_{\bigcirc O}P = |C'P||C''P| = |D'P||D''P|=|AP|^2 \quad\to\quad \begin{cases}|C'P||C''P|=|CP|^2\\[4pt] |D'P||D''P|=|DP|^2 \end{cases} $$ Introduce $\bigcirc PC'D''$, and note $$\begin{align} pow_{\bigcirc P} C'' &= |C''P|^2-|CP|^2 \\[4pt] &=|C''P|^2-|C'P||C''P| \\[4pt] &=|C''P|(|C''P|-|C'P|) \\[4pt] &=|C''P||C''C'| \\[4pt] &=pow_{\bigcirc PC'D'}C'' \end{align}$$ Similarly, we have $pow_{\bigcirc P}D'=pow_{\bigcirc PC'D''}D'$. Since the points $C''$ and $D'$ each have the same powers with respect to $\bigcirc P$ and $\bigcirc PC'D''$, they determine the radical axis of these circles. On the other hand, points $C'$ and $D''$, as the endpoints of the common chord of $\bigcirc O$ and $\bigcirc PC'D''$, determine the radical axis of those circles.
Thus, the point $X$, where these axes meet, has the same power with respect to $\bigcirc P$ and $\bigcirc PC'D''$, and the same power with respect to $\bigcirc PC'D''$ and $\bigcirc O$. Transitively, it has the same power with respect to $\bigcirc P$ and $\bigcirc O$, and so it must lie on the radical axis of these circles, which is the line of the common chord $\overline{AB}$. $\square$
