0

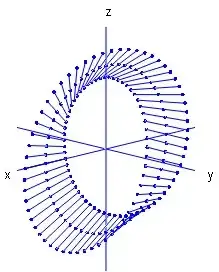
A line segment AB joining the points $A(10,0,0)$ & $B(20,0,0)$ is rotated about the y-axis through an angle of $2\pi$ & simultaneously it rotated through an angle of $\pi$ about its mid point in the plane containing it & the axis of rotation (i.e. y-axis). Find the parametric equation of surface generated if forms of coordinates $$ X,Y, Z $$
My Try: for complete rotation about y-axis in X-Z plane & half rotation , I have $$X=r\cos \theta, Z=r\sin\theta $$
where, $10\leq r\leq 20 $, $0\leq \theta\leq 2\pi $

for secondary rotation I get y-coordinate $$Y=\frac{(20-10)}{2}\sin\frac{\theta}{2}=5\sin\frac{\theta}{2}$$ I don't know if I am correct. Please help me solve this problem. Thanks

1 Answers1

0

The result is a "Möbius strip" as shown here :

enter image description here

You have more or less found the different elements for a natural parametrization.

The final step is made clear if one adopts this matrix-vector formulation :

$$\begin{pmatrix}X\\Y\\Z\end{pmatrix}=\underbrace{\begin{pmatrix}\cos\theta&0&-\sin\theta\\ 0&1&0\\ \sin\theta&0& \ \ \cos\theta\end{pmatrix}}_{R_{\theta}} \underbrace{\begin{pmatrix}15+u\cos(\theta/2)\\ u\sin(\theta/2)\\0\end{pmatrix}}_V \ \ \text{for} \ \ \begin{cases} \ \ \ 0 \leq \theta \leq 2 \pi\\-5\leq u \leq 5\end{cases}$$

otherwise said :

$$\begin{pmatrix}X\\Y\\Z\end{pmatrix}=\begin{pmatrix}(\cos\theta)(15+u\cos(\theta/2))\\ u\sin(\theta/2)\\ (\sin\theta)(15+u\cos(\theta/2))\end{pmatrix} \ \ \text{for} \ \ \begin{cases} \ \ \ 0 \leq \theta \leq 2 \pi\\-5\leq u \leq 5\end{cases}$$ where

  • $R_{\theta}$ is the rotation matrix of angle $\theta$ around $y$ axis,

  • $V$ accounts for the line segment of length $10$ turning "at half-speed" around its midpoint $(15,0,0)$ in the $x0y$ plane (this is maybe the most notable thing to understand), where $u$ allows to sweep each segment for a fixed $\theta$.

The Matlab program for the figure:

   view([20,18]);
   ub=-5;ue=5;
   for t=0:pi/30:2*pi
       Ry=[cos(t),0,-sin(t);
       0,1,0;
       sin(t),0,cos(t)];
       V=[15+ub*cos(t/2),15+ue*cos(t/2);
          ub*sin(t/2),ue*sin(t/2);
          0,0];
       W=R*V;
       plot3(W(1,:),W(2,:),W(3,:));
   end;
Jean Marie
  • 88,997