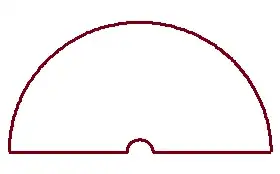
Suppose I have a convergent definite integral of the form $$\int_{-\infty}^\infty \frac{f(x)}{x^2(e^x-1)}\text{d}x,$$ where $f(x)$ has no poles, and I want to try to evaluate it using the residue calculus. I can choose the semi-circular contour $\Gamma$ with positive orientation consisting of paths $\gamma_1 = z$, for $-R\leq z\leq R$, and $\gamma_2=Re^{i\theta}$, for $0\leq\theta\leq\pi$.
Assuming the integral over $\gamma_2$ is zero, then am I right in thinking that the integral is equal to $2\pi i$ times the sum of the residues of the integrand, and that the poles occur at $x=2\pi i k$, where $k\geq 0$ is an integer?
It is this last part I am unsure of. Is this the correct way to consider the poles and calculate the residues?