1

I was teaching my sister indices a while back. Then after covering a few laws of indices she came up with this equation from the top of her head.

$49^x-42^x=-7$

Of course I couldn't solve it. I figured the answer(s) is in $\mathbb{C}$ since $f(x)=49^x-42^x+7$ does not cross the x axis at all.

The best I could do was shrink this down to:

$7^x(7^x-6^x)=-7$

Is there a way to do this or is it outright impossible. I'm also kind of a beginner in complex analysis so I'm curious to know if the answer isn't as complicated as I think it is.

Community
  • 1
Nεo Pλατo
  • 1,745
  • 8
  • 19

3 Answers3

3

From $7^x(7^x-6^x) = -7$, since $7^x > 0$ for all $x$ and $7^x > 6^x$ for $x>0$, the left-hand side is positive for all $x>0$, so there is no solution when $x > 0$. $x = 0$ is not a solution. For $x < 0$, the left-hand side is the product of $7^x \in (0,1)$ and $7^x - 6^x \in (-1,1)$, so can never be as large in magnitude as $\pm 7$. Thus, there is no solution in the reals.

In the complexes, \begin{align*} 49^x - 42^x &= 2\mathrm{i} \cdot \frac{1}{2\mathrm{i}} \left(\frac{49^x}{49^{x/2} 42^{x/2}} - \frac{42^x}{49^{x/2} 42^{x/2}}\right) 49^{x/2} 42^{x/2} \\ &= 2\mathrm{i} \cdot \frac{1}{2\mathrm{i}} \left(\frac{49^{x/2}}{42^{x/2}} - \frac{42^{x/2}}{49^{x/2}}\right) (49 \cdot 42)^{x/2} \\ &= 2\mathrm{i} \sin \left(\frac{-\mathrm{i}}{2}\ln(49/42) x \right)(49 \cdot 42)^{x/2} \end{align*} and replacing the original left-hand side with this, it is straightforward to solve for $x$.
Was missing the $x$ in the sine when I left for lunch. Realized during and corrected now. So this doesn't work.

OP's request for Midgardians: One definition for the complex sine is $$ \sin(z) = \frac{\mathrm{e}^{\mathrm{i}z} - \mathrm{e}^{-\mathrm{i}z}}{2\mathrm{i}} \text{.} $$ Notice that this is the difference of two reciprocals divided by $2\mathrm{i}$. Then \begin{align*} \frac{49^{x/2}}{42^{x/2}} &= \exp \left( \ln\left( \frac{49}{42} \right) \right)^{x/2} \\ &= \exp\left( \frac{1}{2} \ln(49/42) x\right) \\ &= \exp\left(\mathrm{i} \frac{-\mathrm{i}}{2} \ln(49/42) x\right) \end{align*} and the other term is the reciprocal of this one.

Eric Towers
  • 70,953
  • 1
    Well, he figured out already that the answer should be in $\Bbb C$... (Still editing) – dan_fulea Apr 02 '20 at 17:54
  • @dan_fulea : He gave a graphical argument; I gave a symbolic argument. Having two arguments is not a bad thing. – Eric Towers Apr 02 '20 at 17:55
  • 1
    Why is $\frac{49^{x/2}}{42^{x/2}} - \frac{42^{x/2}}{49^{x/2}}$ constant? I think you forgot an $x$ in $\sin \frac{x}{2}\log(49/42)$; the equation is not that straightforward - it has infinitely many roots sure – Conrad Apr 02 '20 at 18:15
  • @ Eric Towers it's not really that straightforward, but barely doable. I'll use it as soon as I figure out what you did. – Nεo Pλατo Apr 02 '20 at 18:22
  • 3
    Ok I got most of it. Just please elaborate for us Midgardians how $\left(\frac{49^{x/2}}{42^{x/2}} - \frac{42^{x/2}}{49^{x/2}}\right)$ became $\sin \left(\dfrac{1}{2}\ln \left(\dfrac{49}{42} \right) \right)$ – Nεo Pλατo Apr 02 '20 at 18:26
  • @EricTowers I tried to check the final formula $$49^x-42^x=2\mathrm{i} \color{red}{\sin \left(\frac{1}{2}\ln(49/42) \right)}(49 \cdot 42)^{x/2}$$ in $x=0$. Is the red constant zero or not?! (If it is zero, then indeed the function $x\to 49^x-42^x$ takes real values on $\Bbb R$, but this contradicts the discussion for $x\in\Bbb R$ at the beginning of the answer. But if it is indeed zero, i change my mind and take $x=1$ to check this formula.) – dan_fulea Apr 02 '20 at 19:15
  • @dan_fulea Of course it's not $0$. Check it on your calculator. Eric made a mistake. – Robert Israel Apr 02 '20 at 19:31
  • @Conrad : Yup. Dropped the $x$ in my haste to leave for lunch. Fixed. – Eric Towers Apr 02 '20 at 19:40
  • @dan_fulea : @RobertIsrael is right; I dropped the $x$. Fixed. – Eric Towers Apr 02 '20 at 19:41
  • @Plato : Explanation (with correct inclusion of $x$) for Midgardians added. – Eric Towers Apr 02 '20 at 19:49
  • Thank you. I'd upvote your answer twice if I could – Nεo Pλατo Apr 02 '20 at 19:50
  • I will drop a final comment, so that my point is explicitly written down. There are often a lot of quick answers (to non-obvious questions, such that are obviously not obvious). This is not profitable for the community. It gives to the maths the competition, not the depth / structure / right way to see things. This is not off-topic, since it applies perfectly for this post. The question is "is it a way to do this [solve...]"? This answer was 3x changed, it still has a false formula (take real x) (as the 1 for the sine, with exp growth on IR), is accepted, does not answer the "way to do this". – dan_fulea Apr 03 '20 at 08:18
2

There are in fact infinitely many complex solutions, which appear to all be in the strip $0.3 \le \text{Re}(z) \le 1$.

Here is a plot of some of them:

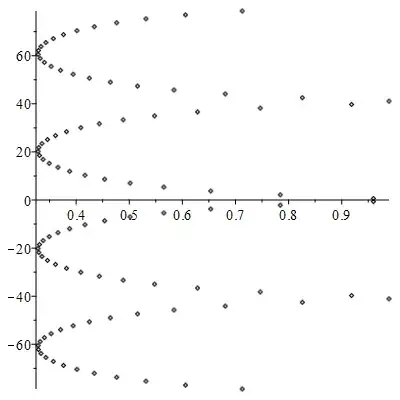
enter image description here

Here is a proof that there are infinitely many. Consider the function $$f(z) = 49^z - 42^z = 42^z ((49/42)^z - 1) $$ This is an entire function, and $f(z+ip) = 42^{ip} f(z) \tag{1}$ where $p = 2 \pi/ \ln(49/42)$. It has an essential singularity at $\infty$. By the Great Picard Theorem, $f$ takes all complex values, with at most one exception, in any neighbourhood of $\infty$. But by (1), if $w$ is an exception then so is $42^{ip} w$. Since there is at most one exception, it can't be any nonzero value (in fact $0$ is not an exception either).

EDIT: By considering $|f(z)|$, it's easy to see the roots are on the curve (with $z = x + i y$) $$ 42^{2x} + 49^{2x} - 2 (42\cdot 49)^x \cos(y \ln(7/6)) = 49$$ and since $-1 \le \cos(y \ln(7/6)) \le 1$ we find that the upper bound for $x$ is indeed $1$ (as for $x=1$ and $\cos(y \ln(7/6))$ the $0$), while the lower bound is the positive real solution of $49^x + 42^x = 7$, approximately $0.328316268$, which doesn't appear to have a closed form.

Robert Israel
  • 470,583
  • one doesn't need to use Great Picard, Hadamard factorization (which imho is easier but of course that's a matter of taste) is enough as the function is of integral order one and it is easily seen not be an exponential; also by a little manipulation one can reduce it to $7^z+7^{1-z}-6^z=0$ and that confirms your observation – Conrad Apr 02 '20 at 19:37
1

I mentioned the need for numerical methods: worse still, there's a lot more than one solution in $\Bbb C$, making this harder to explore. For what it's worth, I wrote some Python to seek a solution by Newton-Raphson. (The code prints pairs of values of $x,\,49^x-42^x+7$ for a while; when it stops, the first value is an approximate root and the second value is very small.) It was approximately $0.501692581938923+7.016931344755486j$ (note $j$ is used in Python instead of $i$). However, multiple solutions exist; when I ran again, I got $0.9889567094750864-41.09191927909876j$.

J.G.
  • 118,053