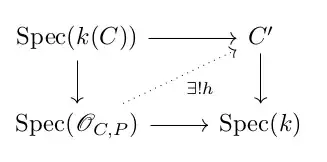Rational map of curves extends to a morphism if $C$ regular

Question

Let $f: C \dashrightarrow C'$ a rational map between curves. A curve is defined as proper $k$-scheme of dimension one. $k$ is the base field. Assume $C$ is regular curve. That means that for every point $a \in C$ the stals $\mathcal{O}_{C,a}$ is a dvr.

Why $f$ extends to a morphism $f: C \to C'$ from viewpoint of 'modern' algebraic geometry.

I explicitly pointed out the word 'modern' since I found here: What is the intuition behind the statement "A rational map from a smooth curve can be extended to a regular one"?

a 'variety style' argument which not satisfies me. It works by choice of an embedding $C' \subset \mathbb{P}^n_k$. Naively or in old school manner rational map $f$ is defined by $x \mapsto [f_0(x):... f_n(x)]$ for $f_k \in K(C)$. Then we can simply extend $f$ to morphism 'pointwise' for every $x \in C$ by 'clearing the denominators' by dividing an appropriate power of the uniformizer $\pi_x \in \mathcal{O}_{C,x}$.

Can this 'variety' argument be modified or extended to show formally correctly that $f$ extend to morphism in light of modern algebraic geometry; that is as a morphism of schemes?

Here what I tried:

Assume, we fix an embedding $j: C' \subset \mathbb{P}^n_k$. It is defined up multiplication by elements from $k^*$ by the 'vector' $(h_0,...,h_n)$ with $h_k \in K(C)$. That's why we can suggestively write $[h_0:...h_n]$. Composition $jf: C \dashrightarrow \mathbb{P}^n_k$ is a rational map defined by $[f_0:...:f_n]$ where $f_j$ is the image of $h_j$ under induced map $f_K: K(C') \to K(C)$. I see two problems: extends $jf$ to a morphism $\bar{jf}:C \to \mathbb{P}^n_k$ and if yes: does the extension factorize over $C'$? To solve the first problem I have to prove that for every $x \in X$ there exist $j=j(x)$ with $f_j(x) \neq 0$ in $\kappa(x)$. Or I need to modify all $f_j$ simultaneously to kill the zeros. That is if $f_j(x)=0$ for all $j \le n$ I can as for varieties simply divide all $f_j$ simultaneously by a power of uniformizer $\pi_x \in \mathcal{O}_{C,x}$ or appropriate order. Since $f$ is a priori not defined in a finite number of points I can repeat this procedure and finish it after finite number of steps. This modification of the $f_j$ induces the extension of $jf$ to a morphism $\bar{jf}: C \dashrightarrow \mathbb{P}^n_k$. Is the argument ok? Now I have to show that $\bar{jf}$ factorize over $C'$. How to show it? I don't know...

Answer 1

A way to prove it is via the valuative criterion for properness.

Assume that $C$ is a regular irreducible curve, $C'$ is proper over $k$ and let $U$ be the maximal dense open subset of $C$ such that $f$ is defined over $U$, say by a morphism $g:U\rightarrow C'$. Let $P\in C-U$ be a closed point: regularness at $P$ implies that $\mathscr{O}_{C,P}$ is a DVR. Then, the valuative criterion of properness gives a morphism $h:\mathrm{Spec}(\mathscr{O}_{C,P})\rightarrow C'$ embedded in the following commutative diagram :

where the upper arrow is the composite $\mathrm{Spec}(k(C))\rightarrow U\xrightarrow{g} C'$, the lower one is given by the inclusion $k\rightarrow\mathscr{O}_{C,P}$ and the left one is given by the inclusion $\mathscr{O}_{C,P}\rightarrow k(C)$.

Then, one may extend $h$ to a morphism $l:V\rightarrow C'$ on an open neighbourhood $V$ of $P$. Since $l$ and $g$ are generically equal, one concludes that $g$ and $l$ represent the same rational map, so that $P\in V\subseteq U$. This proves that $U=C$.

Note that one doesn't need $C'$ to be a curve and the properness condition on $C$ is unnecessary. Besides, the irreducibility assumption on $C$ is also unnecessary : using that $C$ is smooth, one may write it as a disjoint union of its irreducible components and the previous argument works on each irreducible component.