How to interpret this definition of adjoint functors?

Question

Firstly consider the four definitions in the question: How to define rigorously [...].

Also consider the following definition:

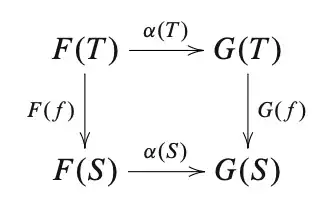
Definition: Let $C,D$ be two categories and $F,G:[C]\to [D]$ be two functors. Suppose that $\alpha:F\to G$ is a morphism of functors $F$ and $G$. We say that $\alpha$ is a functorial in $S$ if, for all $T\in \text{Obj}(C)$ and $f\in \text{Hom}_C(T,S)$, the following diagram commutes:

---

The book "Manifolds, Sheaves, and Cohomology" (written by Torsten Wedhorn) gives the following definition of adjoint functors:

Definition: Let $C,D$ be two categories and let $F:[C]\to [D]$ and $G:[D]\to [C]$ be functors. Then $G$ is said to be right adjoint to $F$ and $F$ is said to be left adjoint to $G$ if for all $X\in\text{Obj}(C)$ and $Y\in\text{Obj}(D)$ there is a bijection

$$\text{Hom}_C(X,G(Y))\cong \text{Hom}_D(F(X),Y),$$

which is functional in $X$ and in $Y$.

Sincerely, I didn't understand the definition above. I tried to use a bijection $\Gamma:\text{Hom}_C(X,G(Y))\to \text{Hom}_D(F(X),Y)$ to construct a morfism of functors which is functorial in $X$ but I was unable to do this.

In view of the definitions of morphism of functors and functorial in a set, the definition above makes no sense to me.

MY QUESTION: What, possibly, did the author of that book mean by that definition?

Answer 1

A correction to start: you've copied the first definition incorrectly. $\alpha$ is not assumed to be a morphism of functors. Instead, $\alpha$ is assumed to be a family of morphisms (in $D$) $\alpha(S)\colon F(S)\to G(S)$, for all objects $S$ in $C$. If the family $\alpha$ is functorial in $S$, then we call $\alpha$ a morphism of functors $F\to G$.

Another comment here: What Wedhorn calls "functorial in $S$" is what most people would call "natural in $S$". A morphism of functors is often called a "natural transformation".

Now based on the very very brief introduction to categories and functors given in the pages leading up to the definition of adjoint functors, you're right to be confused at this point by what Wedhorn means when he writes that a bijection is "functorial in $X$ and $Y$". Here's what's going on:

Given a pair of functors $F$ and $G$ and objects $X$ in $C$ and $Y$ in $D$, we can consider the set $\text{Hom}_C(X,G(Y))$. If we fix $X$ and let $Y$ vary, we can check that we get a functor $\text{Hom}_C(X,G(-))\colon D\to \mathsf{Set}$.

Edit: More precisely, this functor sends an object $Y$ in $D$ to the set $\text{Hom}_C(X,G(Y))$. Given a morphism $\psi\colon Y\to Z$ in $D$, the functor $G$ gives us a morphism $G(\psi)\colon G(Y)\to G(Z)$ in $C$, and we can compose an arbitrary morphism $f\colon X\to G(Y)$ with $G(\psi)$ to get a morphism $G(\psi)\circ f\colon X\to G(Z)$. This is how the functor acts on morphisms: it sends $\psi\colon Y\to Z$ to the map of sets $\text{Hom}_C(X,G(Y))\to \text{Hom}_C(X,G(Z))$ given by $f\mapsto G(\psi)\circ f$.

On the other hand, if we fix $Y$ and let $X$ vary, then we get a functor $\text{Hom}_C(-,G(Y))\colon C^{\text{op}}\to \mathsf{Set}$. (Note the $\text{op}$! This is a contravariant functor from $C$ to $\mathsf{Set}$, with the action on morphisms $\psi$ given by precomposition with $F(\psi)$ instead of postcomposition.)

You can also think of $\text{Hom}_C(-,G(-))$ as a functor $C^{\text{op}}\times D\to \mathsf{Set}$, where the domain is the product category - but it's not necessary.

Similarly, $\text{Hom}_D(F(X),-)$ is a functor $D\to \mathsf{Set}$ for fixed $X$, $\text{Hom}_D(F(-),Y)$ is a functor $C^{\text{op}}\to \mathsf{Set}$ for fixed $Y$, and $\text{Hom}_D(F(-),-)$ is a functor $C^{\text{op}}\times D\to \mathsf{Set}$.

Ok, now we have a bijection $\alpha(X,Y)\colon \text{Hom}_C(X,G(Y))\to \text{Hom}_D(F(X),Y)$ for all $X$ and $Y$. To say that this family of bijections is natural in $Y$ is to say that for fixed $X$, the family $\alpha(X,-)\colon \text{Hom}_C(X,G(-))\to \text{Hom}_D(F(X),-)$ is a morphism of functors (i.e. it's "functorial"/"natural" in $Y$: lots of "naturality squares" squares commute). Similarly, "natural in $X$" means that for fixed $Y$, the family $\alpha(-,Y)\colon \text{Hom}_C(-,G(Y))\to \text{Hom}_D(F(-),Y)$ is a morphism of functors.

Getting your mind wrapped around all of this takes some doing, and it's best to look at a bunch of examples. This is why I recommended in my comment on your previous question that you pick up an introductory category theory book, which will probably be much easier to learn from.

Answer 2

I might be off topic since I am not focusing on this particular definition of an adjoint pair. But let me add something to the big picture by explaining other related concepts. I teach this subject (and stile learning) myself and though, sharing my view would be beneficial for you as well. Suppose we have two categories $\mathcal{C}$ and $\mathcal{D}$ that looks similar to each others. Now we need to compare them and say whether they are actually equal or not. So, first we need a notion of equality for categories. Roughly, there are few different way to establish such a notion. If you like an analogy think of homeomorphisms, homotopies and continuous maps between topological spaces.

1. Isomorphism of categories
   I will begin with the strongest notion which is literally the meaning of an isomorphism. In this case we have pair of functors $\mathcal{F} :\mathcal{C}\to\mathcal{D}$ and $\mathcal{G} :\mathcal{D}\to\mathcal{C}$ which are mutually inverse to each other. That is, once we compose them we get what we would expect $\mathcal{F}\mathcal{G}=1_{\mathcal{D}}$ and $1_{\mathcal{C}}=\mathcal{G}\mathcal{F},$ where $1\text{_}$ means the identity functor.

2. Equivalence of categories
   Isomorpihsm is a very expensive condition on two categories and it occurs rarely in category theory. One the guiding principal in category theory is we should not speak about equality, but isomorphisms. Hence in this diluted notion of isomorphisms, we replace above two equalities by two isomorphisms of functors. Thus we have two natural isomorphisms $\epsilon :\mathcal{F}\mathcal{G}\to1_{\mathcal{D}}$ and $\eta:1_{\mathcal{C}}\to\mathcal{G}\mathcal{F}.$ Given two categories and a candidate functor between them, there is an easy way to determine whether they are equivalent without actually finding the weak inverse.

3. Adjoint functors
   In this final, very weak, but the most common notion we replace above two natural isomorphisms by two natural transformations (+ a mild compatibility condition) called "unit" and "counit" respectively. Furthermore, every adjunction induces an equivalence between certain subcategories. There are few equivalent ways to say whether two functors and adjoint to each others and each way reveals a different prospective of the underlying phenomena. The definition subject to your question is a one such formulation of adjoint pairs. Some times adjoint functors behaves in unexpected ways.

This is by no mean an answer to your question, obviously too long for a comment. Good luck with your studies.

Answer 3

In this answer I will show how I am interpreting that definition after seeing Alex Kruckman's answer.

First, I will make small changes to two definitions that I gave.

Definition 1: Let $C,D$ be two categories and $F,G:[C]\to [D]$ be two functors. A correspondence $\alpha:\text{Obj}(C)\to \text{Mor}(D)$ is said to be a family of morphisms between $F$ and $G$ if, for all $X\in\text{Obj}(C)$, we have $\alpha(X)\in\text{Hom}_D(F(X),G(X))$. In this case we denote $\alpha$ by $\alpha:F\to G$.

---

Definition 2: Let $C,D$ be two categories and $F,G:[C]\to [D]$ be two functors. Suppose that $\alpha:F\to G$ is family of morphisms between $F$ and $G$. We say that $\alpha$ is a functorial in $S$ if, for all $T\in \text{Obj}(C)$ and $f\in \text{Hom}_C(T,S)$, the following diagram commutes:

---

Now I'll show how I'm interpreting that definition in the question.

Notation: To simplify the notation I'll write $C(A,B)$ in the place of $\text{Hom}_C(A,B)$.

Definition 3: Let $C,D$ be two categories. Suppose that $F:[C]\to [D]$ and $G:[D]\to[C]$ are two functors. Observe that, given any $X\in\text{Obj}(C)$ and $Y\in\text{Obj}(D)$, we have that

I) The correspondence $C(X,G(-)):[D]\to \left[\text{Set}\right]$ defined by

$C(X,G(\psi))=\begin{cases} C(X,G(\psi)),&\psi \in \text{Obj}(D)\\ C(X,G(Y))\to C(X,G(Z)),\, f\mapsto G(\psi)\circ f,&\psi \in D(Y,Z) \end{cases}$

is a functor between $D$ and $\text{Set}$;

II) The correspondence $C(-,G(Y)):[C^{op}]\to \left[\text{Set}\right]$ defined by

$C(\psi,G(Y))= \begin{cases} C(\psi,G(Y)),&\psi\in \text{Obj}(C^{op})\\ D(F(Z),Y)\to D(F(X),Y),\, f\mapsto f\circ F(\psi),&\psi \in C^{op}(Z,X) \end{cases}$

is a functor between $C^{\text{op}}$ and $\text{Set}$;

III) The correspondence $D(F(X),-):[D]\to \left[\text{Set}\right]$, defined analogously to item I, is a functor between $D$ and $\text{Set}$;

IV) The correspondence $D(F(-),Y):[C^{op}]\to\left[\text{Set}\right]$, defined analogously to item II, is a functor between $C^{\text{op}}$ and $\text{Set}$.

Then, $G$ is said to be right adjoint to $F$ and $F$ is said to be left adjoint to $G$ if, for all $X\in\text{Obj}(C)$ and $Y\in\text{Obj}(D)$,

1. There is a family $\alpha:C(-,G(Y))\to D(F(-),Y)$ of morphisms between $C(-,G(Y))$ and $D(F(-),Y)$ such that $\alpha$ is functorial in $X$ and $\alpha(X):C(X,G(Y))\to D(F(X),Y)$ is a bijection;
2. There is a family $\beta:C(X,G(-))\to D(F(X),-)$ of morphisms between $C(X,G(-))$ and $D(F(X),-)$ such that $\beta$ is functorial in $Y$ and $\beta(Y)=\alpha(X)$.

---