Just as mentioned in a similar question, in Euclidean plane, there exist space-filling curves that fills the whole plane. So for hyperbolic plane, do there exist some space-filling curves?
Asked
Active
Viewed 562 times
2 Answers
2
I can show the existence of a space-filling curve, assuming space-filling curves exist on the Euclidean plane.
Take the Euclidean plane and use a continuous bijective map on each $x$ and $y$ dimensions using $f(x) = -\log\left(\frac{1}{x}\right)$ to get the open square region. Now we use another continuous bijective map to turn the open square region into an open disc. This is trivial because we just consider the distances from the center and scale them appropriately.
Finally, we just use the Poincare disk model to project the open disc onto the hyperbolic plane.
In this way, we have a continuous bijective map from the Euclidean plane to the hyperbolic plane, so any space-filling curve on the Euclidean plane has a corresponding space-filling curve in the hyperbolic plane.
zhuli
- 2,768
-
maybe the first step is tanh? – Mountain Mar 18 '20 at 17:34
-
2This seems a bit like cheating though: because at any scale, for any $\epsilon>0$, there exists a radius beyond which the spacing between segments exceeds $\epsilon$. Are there curves that fill the hyperbolic plane uniformly, that aren’t concentrated in a small neighborhood? – TLDR Apr 05 '23 at 18:36
2
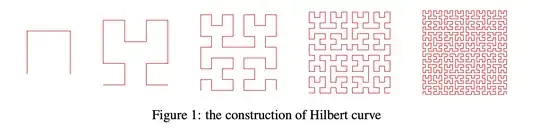
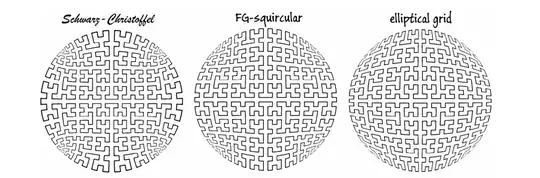
Inspired by Zhuli's answer, We can just conformally map the Hilbert curve from the unit square into the unit disc directly. And then, the unit disc can be treat as Poincare disc which is a model of Hyperbolic plane.
In Chamberlain Fong's article The Conformal Hyperbolic Square and Its Ilk , he gave the example of mapping Hilbert curve into a circular disc by different conformal mappings.
Another interesting question may arise: how about the perpendicular and parallel relationship of lines after the transformation?
Mountain
- 542