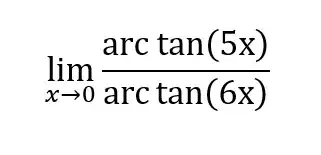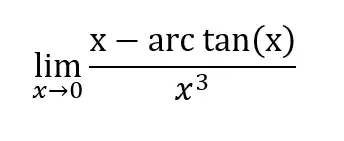3

I am studying limits and how to evaluate them without using l'Hospital Rule or series expansion. Most of them aren't that hard, there are some common trick to do, but I have issues when I face limits of some not-so-common functions such as inverse trigonometric functions.

An example of such a function is this:

enter image description here

And also:

enter image description here

I have no idea how to even approach such a limit so I would be happy if you could, besides just solving these two limits explain some approaches to evaluating limits with inverse trigonometric functions in general.

Jesus
  • 1,888

1 Answers1

3

$$\lim_{x\to0}\frac{\arctan(5x)}{\arctan(6x)} = \lim_{x\to0}\frac{\arctan(5x)}{\arctan(6x)}\cdot\frac{6x}{5x}\cdot\frac56 = \frac56\lim_{x\to0}\frac{\arctan(5x)}{5x}\lim_{x\to0}\frac{6x}{\arctan(6x)}=\frac56$$

Showing $\lim_{u\to0}\frac{\arctan u}{u}=1$

We know that $$\lim_{x\to0}\frac{\tan x }{ x } = \lim_{x\to 0} \frac{x}{\tan x} = 1$$ $$\text{ Now substitute }\tan x = u \implies x = \arctan u \text{ and as } x\to 0 , u = \tan x \to 0 $$

19aksh
  • 12,835
  • 1
    Thank you, but how do I solve the second example? – Jesus Mar 18 '20 at 14:51
  • 1
    @Matthew I'm working on that one. There must be some trick to evaluate it w/o L' Hopital or expansion. – 19aksh Mar 18 '20 at 14:53
  • 1
    It didn't help me, but maybe you will find some use in this limit that looks very similar to the one I'm asking about: https://socratic.org/questions/how-can-i-evaluate-lim-x-0-sinx-x-x-3-without-using-l-hopital-s-rule. – Jesus Mar 18 '20 at 15:02
  • 1
    @Matthew Yeah, I've come across that one, but here it'd become $\arctan 3x$ – 19aksh Mar 18 '20 at 15:06
  • 1
    Someone commented the following link: https://math.stackexchange.com/questions/387333/are-all-limits-solvable-without-lh%C3%B4pital-rule-or-series-expansion, where this exact limit is calculated. Thanks again. – Jesus Mar 18 '20 at 16:23
  • 1
    Nice! It is useful for me too. – 19aksh Mar 18 '20 at 16:29
  • Could you please explain to me the last step he did, in which he went from 3L to 6L? How did he get that fraction inside tan^(-1) ? – Jesus Mar 18 '20 at 16:32
  • 1
    Let us continue this discussion in chat. – 19aksh Mar 18 '20 at 16:42
  • 1
    $$\arctan(2x)- 2\arctan(x) = \arctan(2x) - \arctan(\frac{2x}{1-x^2}) = \arctan\left(\frac{2x-\frac{2x}{1-x^2}}{1+\frac{4x^2}{1-x^2}}\right) = \ \arctan\left(\frac{2x-2x^3-2x}{1-x^2+4x^2}\right) = \arctan\left(\frac{-2x^3}{1+3x^2}\right) $$ – 19aksh Mar 18 '20 at 16:53