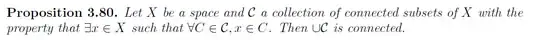This is the problem. I tried doing this using this property but its not working. Can someone help me on this? Any help will be greatly appreciated.
Asked
Active
Viewed 62 times
0
-
1Similar questions have been asked before: https://math.stackexchange.com/questions/2000408/union-of-connected-sets-also-connected has correct answers to a slight generalisation of your question. – Rob Arthan Mar 10 '20 at 22:13
1 Answers
2
Suppose $\bigcup \mathcal{C}= U \cup V$ where $U,V$ are separated subsets.
Suppose WLOG $x \in U$. Then for each $C \in \mathcal{C}$ we know
$$C=(C \cap U) \cup (C \cap V)$$ and these right hand sets are also separated (as subsets of $U$ and $V$ resp.) $x \in U \cap C$ by assumption so the $C \cap V = \emptyset$ or $C$ would be disconnected, which it is not. It follows that $C \subseteq U$.
As $C$ was arbitrary in $\mathcal{C}$, $\bigcup \mathcal{C} \subseteq U$ and $V$ is empty, and so $\bigcup \mathcal{C}$ is connected.
Henno Brandsma
- 250,824
-
1
-
how did you get C = (C $\cap$ U) $\cup$ (C $\cap$ V) ? Is it De-Morgans law? – Math_Is_Fun Mar 11 '20 at 03:50
-
@Math_Is_Fun N0, right to left inclusion is trivial, and if $x \in C$, it's in the union, so in $U \cup V$ etc. – Henno Brandsma Mar 11 '20 at 05:29
-
I got it finally, god knows why I was overthinking on a petty issue. Its a set theoretic statement: A $\cap$(B $\cup$ C) = (A $\cap$ B) $\cup$ (A $\cap $C), se theory its not even topology. lolz :P – Math_Is_Fun Mar 11 '20 at 05:47
-
@Math_Is_Fun in general topology a lot of stuff reduces to set theory. One should know quite a bit about (basic) set theory. – Henno Brandsma Mar 11 '20 at 05:50
-
x∈U∩C by assumption so the C∩V=∅ or C would be disconnected, which it is not. It follows that C⊆U. How did you get this? I know that u assuming x in the intersection of U and C, that means x $\in$ U and x $\in$ C. After that, how did you get C $\subset$ U ? – Math_Is_Fun Mar 11 '20 at 06:01
-
@Math_Is_Fun if $C\cap V$ were non- empty, $C$ would be disconnected, as a union of two non-empty separated sets. But $ C$ is connected so that intersection is empty and so all points of $ C$ lie in $U$, none can be in $V$. – Henno Brandsma Mar 11 '20 at 06:05
-