What's the need to find derivative of a polynomial?

Question

I was learning differential calculus when I came with a doubt that why do we need to find derivative of polynomial. How is it useful?

Answer 1

An example one can find here, but in a simplified presentation.

Suppose we have a have two walls at right angle and we want to delimitate a rectangular area with a $3$ meters long barbed wire fence, knowing that 2 sides of the rectangle are along the wall.

Our objective is to maximize the enclosed area.

Let us denote by $x$ the length in one direction ; therefore, the length in the other direction is $(3-x)$.

A) First approach using polynomial derivation in a blind way :. The area of a rectangle being length $\times$ width, we have to maximize the following function :

$$f(x):=x(3-x)=3x-x^2$$

which will be obtained for the value of $x$ such that $f'(x)=0$ giving $3-2x=0$, i.e., $x=3/2$.

Please note that we are finding that the square is the most advantageous among all rectangular shapes.

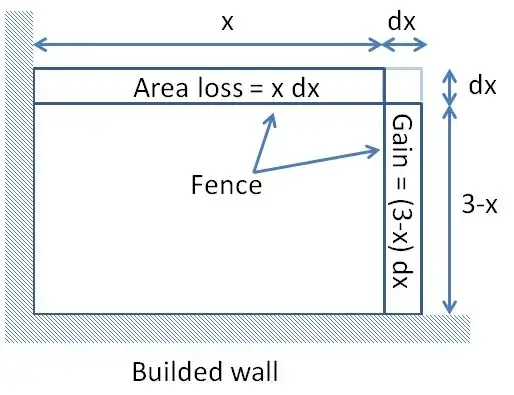
B) Second approach, of a geometrical nature. Consider the figure below :

Extending the length of the fence on the horizontal direction from $x$ to $x+dx$ brings a correlative decrease from $(3-x)$ to $3-x-dx$ in the other direction. Therefore, we have an area gain of $(3-x)dx$ and an area loss of $x dx$. The net gain is :

$$Gain - Loss = (3-x)dx - x dx=\underbrace{(3-2x)}_{f'(x)}dx$$

Expressing that there is an equilibrium (Gain=Loss) is like saying that $f'(x)=0$ !

Moreover, the second order element $dx^2$ which is neglected is vizualized as the small pale blue little square at the upper right corner, reflecting the expansion of :

$$\underbrace{(x+dx)(3-x-dx)}_{f(x+dx)}=\underbrace{x(3-x)}_{f(x)}+\underbrace{(3-x-x)}_{f'(x)}dx-\underbrace{dx^2}_{\text{neglected}}$$

which is a Taylor expansion of function $f$. This expansion proves in particular that :

$$\dfrac{f(x+dx)-f(x)}{dx}=f'(x)-dx$$

Answer 2

$\require{begingroup} \begingroup$ $\def\i{\mathbf{i}}$

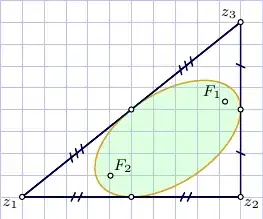
One of the beautiful and somewhat unexpected application of the derivative of a polynomial is Marden’s theorem, gives a geometric relationship between the zeros of a third-degree polynomial with complex coefficients and the zeros of its derivative.

Suppose the zeroes $z_1,\ z_2$, and $z_3$ of a third-degree polynomial $p(z)$ are non-collinear. There is a unique ellipse inscribed in the triangle with vertices $z_1,\ z_2,\ z_3$ and tangent to the sides at their midpoints: the Steiner inellipse. The foci $F_1,\ F_2$ of that ellipse are the zeros of the derivative $p'(z)$.

\begin{align} F_{1,2}&=\tfrac13\,\left(z_1+z_2+z_3 \pm\sqrt{z_1^2+z_2^2+z_3^2-z_1\cdot z_2-z_2\cdot z_3-z_3\cdot z_1}\right) \end{align}

For example, consider a triangle with vertices

\begin{align} z_1&=0 ,\quad z_2=10 ,\quad z_3=10+8\,\i ,\\ p(z)&= (z-z_1)(z-z_2)(z-z_3) =z^3-(20+8\,\i)\,z^2+(100+80\,\i)\,z ,\\ p'(z)&= 3\,z^2-(40+16\,\i)\,z+100+80\,\i =0 ,\\ F_1&=\tfrac13\,\left(20+\sqrt{2\,\sqrt{481}+18} +\i\,\left(8+\sqrt{2\,\sqrt{481}-18}\right)\right) \approx 9.288443511+4.361869847\,\i ,\\ F_2&=\tfrac13\,\left(20-\sqrt{2\,\sqrt{481}+18} +\i\,\left(8-\sqrt{2\,\sqrt{481}-18}\right)\right) \approx 4.044889823+0.971463487\,\i . \end{align}

$\endgroup$

Answer 3

The derivative in any case can be useful in many ways. The most obvious comparison is if you are given a continuous function to represent displacement ($s$) then we can calculate velocity and acceleration by differentiating with respect to time: $$v=\frac{ds}{dt},a=\frac{dv}{dt}=\frac{d^2s}{dt^2}$$ However often other problems require finding the optimum conditions for something to happen, which is represented as a maxima or minima on a graph and hence finding the derivative is used here too.